Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.4 - Ex. 14

Desenhe as lemniscatas nos Exercícios 13-16. Quais simetrias essas curvas têm?

Passo 1

Olá pessoal. Para fazermos curvas polares complicadas, iremos precisar de uma calculadora gráfica ou computador. Se o dispositivo não representa gráficos polares diretamente, podemos converter r = ƒ(u) para a forma paramétrica utilizando as equações:

Em seguida, utilizamos o dispositivo para desenhar uma curva parametrizada no plano cartesiano . Pode ser necessário utilizarmos o parâmetro em vez de para o dispositivo de representação gráfica.

Exemplo: curva lemniscata :

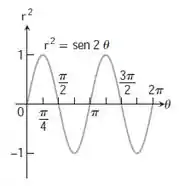
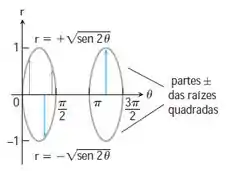
Primeiramente esboçamos o gráfico no plano e ignoramos os valores de para os quais é negativo:

Agora iremos esboçar o gráfico de no plano cartesiano :

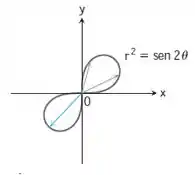
E em seguida desenhamos o gráfico polar:

Passo 2

Porém podemos utilizar o programa computacional WolframAlpha, onde conseguimos obter o seguinte gráfico:

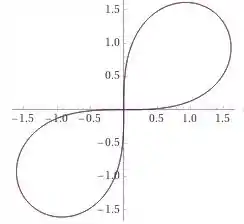
Pelo gráfico podemos observar que há simetria na origem. Além disso, sabemos que a curva é simétrica em relação à origem porque:

Resposta

A curva é simétrica em relação à origem.

Exercícios de Livros Relacionados

Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando t aumenta x = t 3 + t y = t 2 + 2 - 2 ≤t ≤ 2

Descreva o movimento de uma partícula com posição ( x ,y ) quando t varia no intervalo dado y =2 cos ⁡ t x = 5 sin ⁡ t

Descreva o movimento de uma partícula com posição ( x ,y ) quando t varia no intervalo dado y =1 +3 cos ⁡ t x = 2 +sin ⁡ t

Descreva o movimento de uma partícula com posição (x, y) quando t varia no intervalo dado y =cos ² ⁡ t ² x = sin ⁡ t

Use os gráficos de x = f ( t ) e y = g ( t ) para esboçar a curva parametrizada x = f ( t ) e y = g ( t ) . Indique com setas a direção na qual a curva é traçada quanto t aumenta.