Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 20
Descreva o movimento de uma partícula com posição quando varia no intervalo dado
Passo 1
Temos então nessa questão meu querido amigo, que descobrir o formato da curva descrita pela equação paramétrica dada.
Temos então a curva parametrizada por:
E para conseguirmos descobrir o traçado dessa curva, vamos criar um quadro, com diferentes valores para e seus respectivos valores para e . Com isso, teremos diversos pontos a serem plotados num gráfico, e com isso poderemos visualizar melhor qual o comportamento da nossa curva.
Para plotar os pontos e traçar o gráfico eu irei utilizar o GeoGebra, mas você pode escolher outro software que se adeque melhor ao seu uso.
Passo 2
Criando então nossa tabela:
Veja que a nossa curva é limitada:
Então não podemos passar desse intervalo.
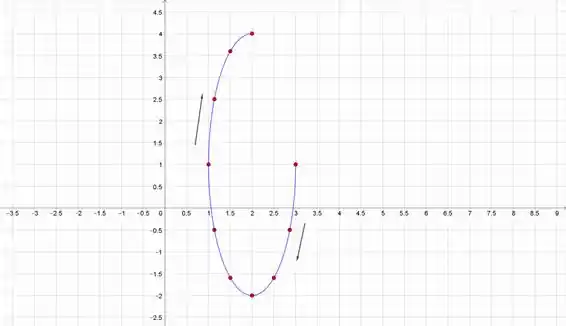
Plote os pontos e desenhe uma curva suave através deles. Note que é uma elipse centrada em . Se , então seria um círculo com raio caso contrário, é a largura máxima e é a altura máxima da elipse. O e podem ser trocados, o que pode mudar a direção em que a curva é desenhada.
A partícula começa em e então se move do caminho ao redor, no sentido horário, na trajetória de uma elipse com centro em , terminando em .
Resposta
