Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.4 - Ex. 20
Encontre os coeficientes angulares das curvas nos Exercícios 17-20 nos pontos determinados. Esboce as curvas com suas tangentes nesses pontos.
Rosa de quatro pétalas ;
Passo 1
Oi galerinha, vem comigo!
Primeiro precisamos relembrar que o coeficiente angular de uma curva polar no plano é dado ainda por , que não é . Para saber por que, pense no gráfico de como o das equações paramétricas:
Se é uma função derivável de , então e também o são e, quando , podemos calcular a partir da fórmula paramétrica:
Então com a equação , podemos escrever da seguinte forma:
Jogando na equação do coeficiente angular, teremos o seguinte:
Passo 2
- Para , temos:
- Para
- Para
- Para
Passo 3
Utilizando o programa computacional WolframAlpha a equação , e definindo as tangentes nesse gráfico, temos:
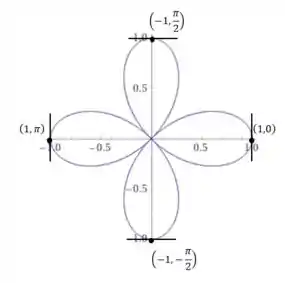
Como podemos observar no Passo 2, e juntamente com o gráfico que obtemos, os coeficiente angulares para quando e não existe, porque forma uma reta perpendicular ao eixo das abscissas.
Até mais galerinha.
Resposta
O coeficiente angular em e em não existe, porque a reta é perpendicular ao eixo das abscissas. Mas, o coeficiente angular em e em é .