Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 49

Desenhe um mapa de contorno da função mostrando várias curvas de nível.

Passo 1

Fala ai, tranquilo?

Nossa missão nesta questão é construir um mapa de contorno.

Vamos começar entendendo o que é um mapa de contorno? 😊

Um mapa de contorno é um gráfico que mostra curvas de níveis de uma função de duas variáveis. Cada cruva de nível conecta pontos no plano onde a função tem o mesmo valor. Isso nos proporciona uma representação visual das variações da função no plano, nos dando padrões e pontos críticos.

Para se desenhar o mapa de contorno, precisa-se chegar à função das curvas de nível.

Basta fazer e depois ir variando (dando valores) para representar algumas curvas de nível no mapa.

Em outras palavras, temos que verificar o comportamento da curva para diferentes valores.

Vamos começar?

Passo 2

Vamos iniciar considerando a função

Isolando

Agora vamos variar os valores de , para chegar ao mapa de contorno.

Passo 3

Para

Passo 4

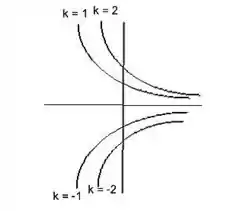
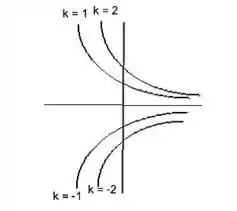
Entendendo um pouco mais a função.

As curvas de nível são hipérboles.
As curvas para são no quadrante superior e decrescem à medida que aumenta.
As curvas para são no quadrante inferior e também decrescem, mas no sentido negativo.
O ponto de corresponde ao eixo , onde.