Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 43
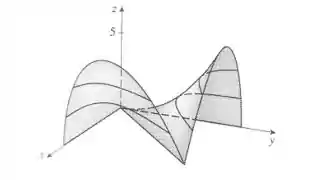
Um mapa de contorno de uma função é mostrado. Use-o para fazer um esboço do gráfico de .
Passo 1
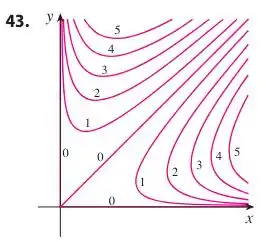
Eaee, belezinha?? Bom... o enunciado nos deus as seguintes curvas de nível de um gráfico:
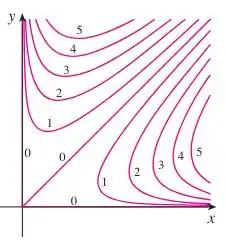
Queremos elaborar o seu gráfico tridimensional.
Para isso, temos que analisar o que acontece quando variamos :
- As curvas de nível mais próximas entre si indicam uma mudança mais rápida na altura ;
- As curvas mais espaçadas indicam uma mudança mais lenta em .
Além disso, perceba que o enunciado nos deu os valores de de cada curva de nível!!! Esses valores irão nos dar ideia de altura no gráfico!! 😉
Agora bora aplicar!! 😉
Passo 2
Bom... vamos analisar o gráfico novamente:
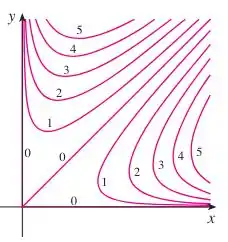
Perceba que quanto mais próximo da origem e dos eixos, a figura tende a zero.
A figura também tenderá a zero próximo da reta .
Perceba também que a figura terá ponto de máxim em .
Com base nisso, e com base também nas relações de mudanças de , obtemos a seguinte figura:
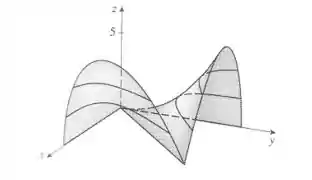
Resposta
