Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.1 - Ex. 43
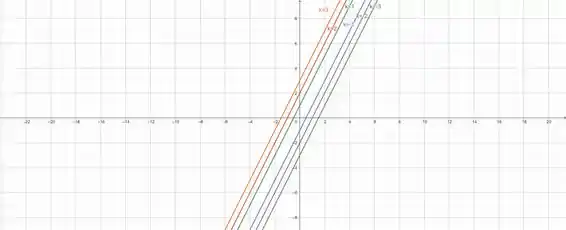
Faça o mapa de contorno da função mostrando várias curvas de nível.
Passo 1
Olá, meu querido amigo. Vou te ajudar a resolver essa atividade.
A gente tem a função dada por:
E precisamos desenhar o seu mapa de contorno. As curvas de nível de uma função de duas variáveis são aquelas com equação , onde é uma constante (na imagem de ).
Como a gente pode ver abaixo, a curva de nível é a planificação de um sólido.
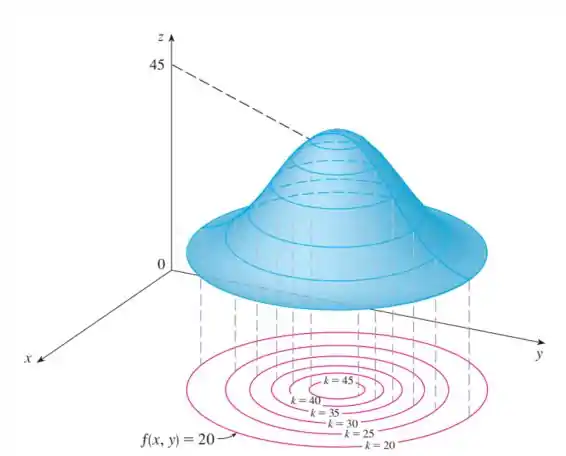
Para se desenhar o mapa de contorno, precisa-se chegar à função das curvas de nível.
Basta fazer e depois ir variando (dando valores) para representar algumas curvas de nível no mapa.
Passo 2
Então vamos iniciar:
Como podemos ter positivos e negativos:
Essa é a equação de uma reta
Onde é o coeficiente angular e é onde a reta toca o eixo .
Variando , chega-se ao seguinte mapa de contorno:
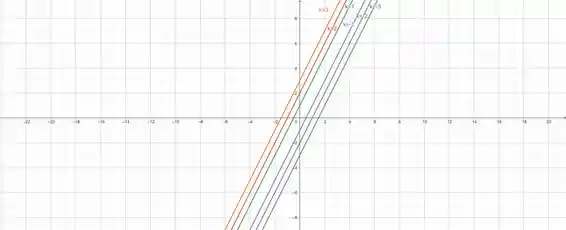
Resposta
