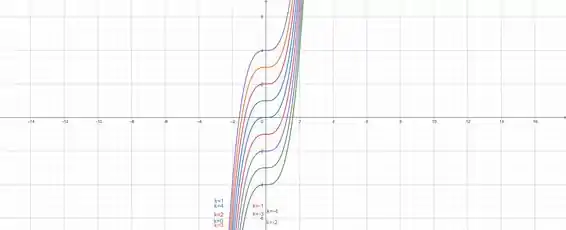
Faça o mapa de contorno da função mostrando várias curvas de nível.
Passo 1
Olá, pronto para mais um dia de aprendizado?
A gente tem a função dada por:
E precisamos desenhar o seu mapa de contorno. As curvas de nível de uma função de duas variáveis são aquelas com equação , onde é uma constante (na imagem de ).
Como a gente pode ver abaixo, a curva de nível é a planificação de um sólido.
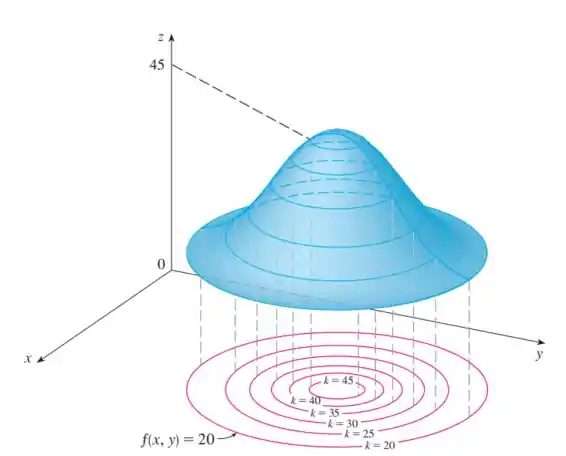
Para se desenhar o mapa de contorno, precisa-se chegar à função das curvas de nível.
Basta fazer e depois ir variando (dando valores) para representar algumas curvas de nível no mapa.
Passo 2
Então vamos iniciar nossa resolução:
- O gráfico de é uma curva cúbica, que é simétrica em relação à origem quando .
- À medida que muda, a curva se desloca verticalmente sem alterar sua forma ou orientação.
Variando , chega-se ao seguinte mapa de contorno:
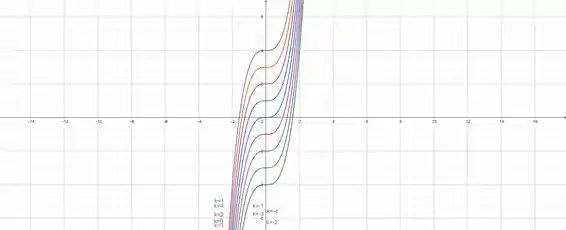
Resposta