Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.7 - Ex. 65

Desenhe as retas e seções cônicas nos Exercícios 65-74.

r = 3 sec ⁡ θ - π 3

Passo 1

Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?

Neste problema, nosso objetivo será usar as transformações de coordenadas polares para coordenadas cartesianas, para encontrar a equação cartesiana da equação polar dada. Para isso podemos fazer uso das seguintes relações:

x = r cos ⁡ θ     e     y = r sen ⁡ θ

Por fim, com auxílio de software, podemos traçar o esboço da equação cartesiana encontrada.

Bora lá?

Passo 2

De início, sabendo que sec ⁡ x = 1 cos ⁡ x , podemos dizer que:

r = 3 sec ⁡ θ - π 3   ⟹ r = 3 c os ⁡ θ - π 3   ⟹ r cos ⁡ θ - π 3 = 3

Veja que a equação encontrada, apresenta uma diferença entre dois arcos, portanto usaremos a seguinte identidade trigonométrica:

cos ⁡ x - y = cos ⁡ x ∙ cos ⁡ y + sen ⁡ x ∙ sen ⁡ y

Logo,

r cos ⁡ θ - π 3 = 3   ⟹ r cos ⁡ θ ∙ cos ⁡ π 3 + sen ⁡ θ ∙ sen ⁡ π 3 = 3  

Aplicando a distributiva, temos:

r cos ⁡ θ ∙ cos ⁡ π 3 + r sen ⁡ θ ∙ sen ⁡ π 3 = 3

Usando as relações citadas no passo 1 e determinando os valores conhecidos, temos:

x ∙ 1 2 + y ∙ 3 2 = 3

Multiplicando ambos os lados por 2 , têm-se:

x + 3 y = 6

Encontramos assim, nossa equação em coordenadas cartesianas e ela representa uma reta.

Passo 3

Agora, traçando o gráfico da equação, com auxílio de um software, obtemos:

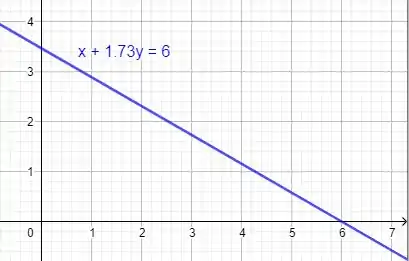
Espero ter ajudado! Abraços e até a próxima!

Resposta

x + 3 y = 6 .

Exercícios de Livros Relacionados

A órbita de Marte em torno do Sol é uma elipse com excentricidade 0,093 e semieixo maior 2,28.10 8k m . Encontre uma equação polar da órbita.
A órbita de Júpiter tem excentricidade 0,0 48 e o comprimento do seu eixo maior é 1,56.10 9k m . Encontre uma equação polar para a órbita.
Marque o ponto cujas coordenadas polares são dadas. A seguir, encontre dois outros pares de coordenadas polares desse ponto, um com r0 e outro com r0 . (a) 2 ,π 3 (b) 1 ,- 3 π 4 (c) - 1 ,π 2
Marque o ponto cujas coordenadas polares são dadas. A seguir, encontre dois outros pares de coordenadas polares desse ponto, um com r0 e outro com r0 . 1 ,7 π 4 - 3 ,π 6 1 , - 1
As coordenadas cartesianas de um ponto são dadas. (i)Encontre as coordenadas polares r , θ . Onde r0 e 0 ≤ θ ≤ 2 π . (ii) Encontre as coordenadas polares r , θ . Onde r0 e 0 ≤ θ ≤ 2 π . ( 3 3 , 3 )( 1