Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 1
Marque o ponto cujas coordenadas polares são dadas. A seguir, encontre dois outros pares de coordenadas polares desse ponto, um com r > 0 e outro com
(a)(b)(c)
Passo 1
Então pessoal, para resolvermos exercícios de coordenadas polares precisamos nos acostumar a escrever os pontos com uma cara nova. No lugar de e que usamos normalmente no plano cartesiano vamos substituir pelo raio e o ângulo . Usando esse novo raciocínio estamos prontos para resolver as primeiras questões.
Passo 2
Na letra (a) temos um raio e um ângulo , equivalente a, É representado pelo gráfico a seguir.
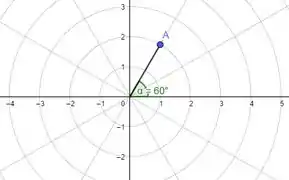
Temos que conseguir outra maneira para representar o ponto com e
Para :
Podemos fazer com que o ângulo fique negativo, ou seja, fazer com que ele “ande” no sentido horário.
A nova coordenada é: .
Para :
Andamos então e aí só inverter o raio.
A nova coordenada é:
Passo 3
Na letra (b) o raio é e o ângulo é de (pelo sinal já da pra sacar que ele tá andando no sentido horário né). Um jeito fácil de enxergar é pensando nesses ângulos com relação ao eixo, como vemos no desenho.
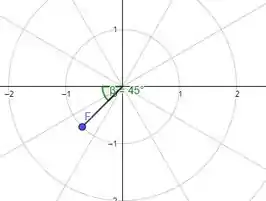
Na letra (b) temos que conseguir outra maneira para representar o ponto com e
Para :
Já temos uma coordenada com raio positivo e eixo negativo, agora dá pra pensar em representar os dois elementos positivos. O ângulo será positivo ao fazer com que ele “ande” no sentido anti-horário.
A nova coordenada é: .
Para :
Para o raio negativo agora tá fácil, sabemos que é só jogar o raio para o lado oposto.
A nova coordenada é: .
Passo 4
A letra (c) dá um raio negativo e um ângulo reto de
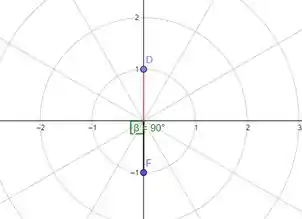
Na letra (b) temos que conseguir outra maneira para representar o ponto com e
Para :
O raio será positivo e andamos meia volta no sentido horário.
A nova coordenada é: .
Para :
O raio será negativo e andamos uma volta completa no sentido anti-horário.
A nova coordenada é: