Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 2
Marque o ponto cujas coordenadas polares são dadas. A seguir, encontre dois outros pares de coordenadas polares desse ponto, um com e outro com
Passo 1
Olá, meu querido amigo. Vou te ajudar a resolver essa atividade hoje.
Aqui a gente tem 3 pontos:
E devemos marcar esses pontos no plano polar. Devemos também procurar pares desses pontos, isso é, pontos opostos a esse, onde o raio será e .
Sabemos que podemos nos mover no círculo trigonométrico no sentido horário e no sentido anti-horário, e é com essa ideia que iremos representar os pontos com os raios opostos, veja que as coordenadas:
E
São os mesmos pontos, agora também podemos fazer:
Então pessoal, primeiramente devemos lembrar que as coordenadas polares têm o seguinte formato:
Ou seja, a primeira coordenada se refere ao raio e a segunda ao ângulo em relação a um referencial (em geral, o eixo ).
Voce pode visualizar melhor como é a relação entre as coordenadas polares e cartesianas, como também sua representação.
Então deveremos utilizar o GeoGebra para colocarmos os pontos que precisamos nos eixos corretos, mas veja que você deve principalmente entender o significado dessa coordenada em relação as coordenadas cartesianas.
O ponto é um local no plano cartesiano representado por sua localização em e em , ao colocarmos em coordenadas polares estamos representando esse mesmo local com a distância da origem e o ângulo que esse faz com a horizontal.
Passo 2
Então na letra (a) que temos raio e ângulo de , equivalente a
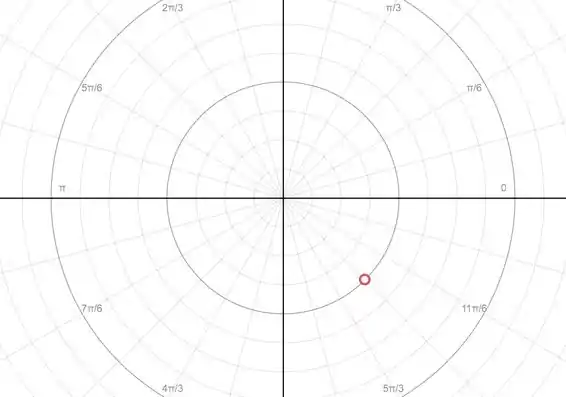
Perceba que podemos escrever o ângulo como em relação ao eixo no quadrante, chegando ao mesmo ponto. Logo outra maneira de representar seria
A segunda forma seria deixando o raio negativo e para isso é só inverter o ângulo para o quadrante oposto, ou seja, se o ângulo está a do eixo no quadrante, o colocamos também a esse ângulo com relação ao mesmo eixo no quadrante.
Então o mesmo ponto seria representado por
Na letra (b) temos O raio é, porém como é negativo iremos calcular no ângulo de e inverter o raio, ficando com:
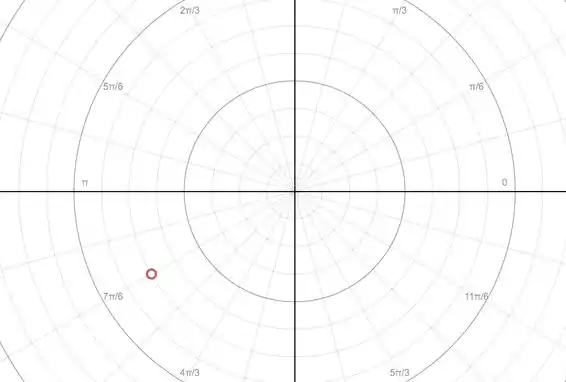
Encontrando o outro ângulo podemos deixar o raio positivo e somar ao ângulo dado, ficando Para outra representação é só usar o raio negativo, somando ao ângulo dado no exercício
Passo 3
Na letra (c) temos raio e um ângulo de rad, diferente do que estamos acostumados a ver (os múltiplos de ). Mas não vamos pular o exercício só por isso. Podemos converter para graus, se achar que isso é um problema. Usando a comparação que rad equivale a chegamos em um ângulo próximo ae aí a representação nas coordenadas polares fica:
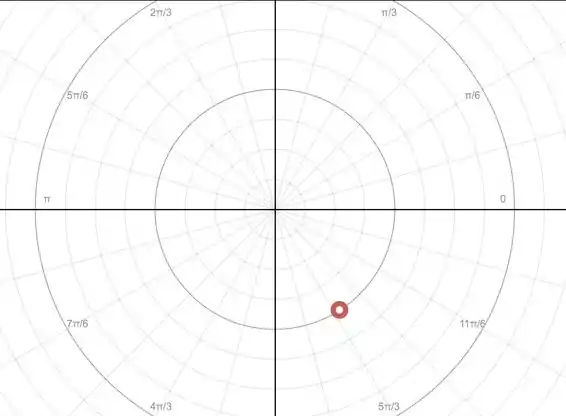
Procurando os outros dois meios de representar achamos o ângulo positivo, que observando na figura seria , ficando ou representando com o raio negativo, isto é, invertendo o ângulo usando a mesma relação com o eixo