Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 6
As coordenadas cartesianas de um ponto são dadas.
(i)Encontre as coordenadas polares Onde e
(ii) Encontre as coordenadas polares Onde e
- (, )
- (,2)
Passo 1
Olá, meu amigo. Vou te ajudar a resolver essa atividade.
Aqui, nós iremos, eu e você, encontrarmos as coordenadas polares dos pontos:
Para isso, iremos utilizar a relação:
Basicamente a gente vai substituir nessas relações, e assim iremos encontrar as coordenadas polares.
Para os raios opostos, a gente vai utilizar do círculo trigonométrico:
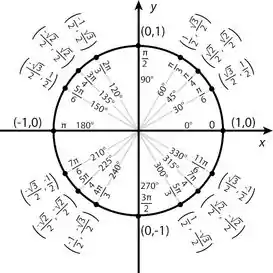
Basicamente existem diversas formas de escrevermos o mesmo ponto em coordenadas polares.
Passo 2
Na primeira coordenada, onde podemos usar a hipotenusa para descobrir o raio, e então:
Agora sabendo o raio podemos usar a relação:
Como tanto seno quanto cosseno é positivo, estão no primeiro quadrante e o ângulo que satisfaz é o de 30º.
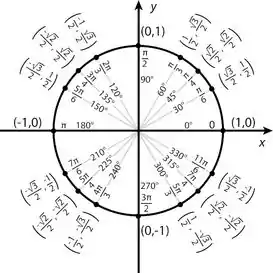
Escrevendo então em coordenadas polares teremos Outra maneira de escrever é usando raio negativo como pede a questão.
Invertendo então o ângulo para o quadrante oposto, teremos o ângulo
e a coordenada fica
Passo 3
Na letra (b) temos Encontrando o raio por meio da fórmula:
Usando então a relação:
Multiplicando a fração por
Como o cosseno é positivo e o seno negativo esperamos que o ponto esteja no 4º quadrante e com com relação ao eixo dos cossenos.
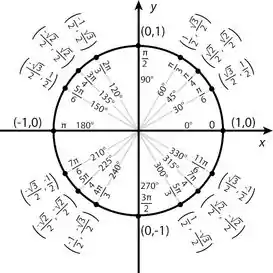
Logo podemos escrever o ponto com o raio positivo ( ou negativo invertendo o ângulo para (subtraindo 180) com relação a origem
Resposta
- (.