Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 70

Desenhe o sólido limitado pelo plano x + y + z = 1 e pelo paraboloide z = 4 - x 2 - y 2 e determine seu volume exato. (Utilize seu SCA para fazer esse desenho, para achar as equações dos limites da região de integração e para calcular a integral dupla).

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O primeiro passo é construir o sólido em questão para analisar os limites de integração:

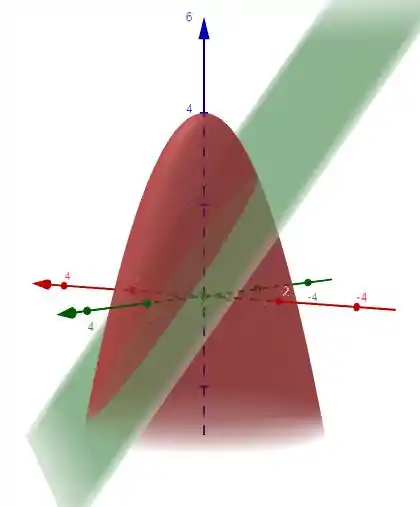
Passo 2

A partir da figura, podemos observar que para a dada região z vai do plano ao fim do paraboloide. Portanto:

1 - x - y ≤ z ≤ 4 - x 2 - y 2

Com um programa podemos ver os pontos de intersecção de x e y portanto, temos:

R = x , y | 1 2 1 - 14 < x < 1 2 1 + 14 , 1 2 - 1 2 13 + 4 x - 4 x 2 < y < 1 2 + 1 2 13 + 4 x - 4 x 2

Bom... nossa integral ficar com essa cara:

∫ 1 2 1 - 14 1 2 1 + 14 ∫ 1 2 - 1 2 13 + 4 x - 4 x 2 1 2 + 1 2 13 + 4 x - 4 x 2 4 - x 2 - y 2 - ( 1 - x - y ) d y d x

Passo 3

Agora é só usar a calculadora gráfica ou algum programa pra resolver essa integral. Temos que:

V = 105 8 π

Resposta

V = 105 8 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral dupla, identificando-a antes com o volume de um sólido. ∬ R3d A, R = x , y- 2 ≤ x ≤ 2,1 ≤ y ≤ 6
Calcule a integral dupla, identificando-a antes com o volume de um sólido. ∬ R( 4 - 2 y )d A, R = 0 ,1 × [ 0 ,1 ]
Calcule a integral dupla, identificando-a antes com o volume de um sólido. ∬ R( 5 - x )d A, R = x , y0 ≤ x ≤ 5,0 ≤ y ≤ 3
Nos Exercícios 19-24, esboce a região de integração e calcule a integral. ∫ 0 π ∫ 0 x x sen ⁡ y d yd x
Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = x , y = 0 e x = 9