Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.2 - Ex. 5c
- Esboce o gráfico da curva plana com a equação vetorial dada.
- Encontre .
- Esboce o vetor posição e o vetor tangente para o valor dado de .
Passo 1
Fala ai pessoal! Belezinha? Vamos resolver a Letra C, a questão nos para apresentarmos o esboço do vetor posição
E o vetor tangente quando .
Para encontrarmos o vetor tangente teremos que dderivar o vetor posição, e substituir . E não vamos esquecer de plotar um gráfico do vetor posição e analisar!
Bora!!!
Passo 2
Para calcular o vetor tangente (ou a derivada da função ), derivamos cada componente da função em relação a :
Galera, a curva é dada pela seguinte equação:
E a derivada da curva é:
Passo 3
O vetor posição em é:
O vetor tangente em da derivada
Passo 4
Como saber a curva formada?
Componente = : Esta componente representa a coordenada da curva em função do parâmetro . Observando a forma , sabemos que cresce exponencialmente à medida que aumenta. Quando , , e à medida que aumenta, cresce rapidamente.
Componente : Esta componente representa a coordenada da curva em função do parâmetro . Observarmos as quesçãoes, sabemos que também cresce exponencialmente à medida que aumenta. Quando , e à medida que aumenta, cresce.
Passo 5
A combinação das componentes e descreve uma curva que se afasta rapidamente do ponto inicial à medida que aumenta. A forma exata da curva pode ser entendida como uma trajetória que se afasta exponencialmente do ponto inicial ao longo do tempo.
Esboçando o gráfico com os vetores posição e tangente, temos:
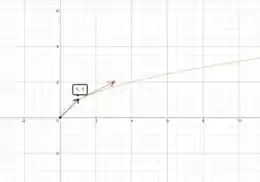
No gráfico acima, o vetor preto é o vetor posição e o vetor vermelho é o vetor tangente.
Resposta
