Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 30

Calcule a integral iterada convertendo para coordenadas polares.

∫ 0 a ∫ - a 2 - y 2   a 2 - y 2   2 x + y d x d y

Passo 1

Oi pessoal, tudo bem? Vamos lá, essa questão não exige muita teoria, foi pedido o cálculo da seguinte integral:

∫ 0 a ∫ - a 2 - y 2   a 2 - y 2   2 x + y d x d y

Em coordenadas polares. Precisaremos então utilizar as relações bases das coordenadas polares para alterar as variáveis e escrever os limites de integração em função de r e θ .

Veja as relações:

x = r cos ⁡ θ

y = r sen ⁡ θ

d y d x = r d r d θ

x 2 + y 2 = r 2

Agora é so fazer as manipulações matemáticas necessárias. Vamos lá então?

Passo 2

Observando os limites de integração sabemos a região de integração:

x = ± a 2 - y 2  

x 2 = a 2 - y 2

x 2 + y 2 = a 2

Sabemos que x 2 + y 2 = r 2 , logo:

r 2 = a 2

r = a

Observando novamente os limites, vemos que y   possui os limites de 0 a a . De forma que nunca possui valores negativos. Temos então que nossa região se parece mais ou menos com isso:

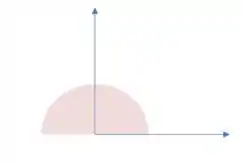
Logo, estamos no primeiro e segundo quadrante com 0 ≤ θ ≤ π .

Onde D será a região delimitada por:

0 ≤ r ≤ a ,   0 ≤ θ ≤ π

Passo 3

Agora é só desenvolver:

∫ 0 a ∫ - a 2 - y 2   a 2 - y 2   2 x + y d x d y

Temos que substituir x , y pe os limites de integração por suas correspondentes em

coordenadas polares.

2 x + y =   2 r cos ⁡ θ + r sen ⁡ θ

E

0 ≤ r ≤ a ,   0 ≤ θ ≤ π

Logo temos:

∫ 0 a ∫ - a 2 - y 2   a 2 - y 2   2 x + y d x d y = ∫ 0 π ∫ 0 a 2 r cos ⁡ θ + r sen ⁡ θ r d r d θ

Fazendo a distributiva com o r .

∫ 0 π ∫ 0 a 2 r cos ⁡ θ + r sen ⁡ θ r d r d θ = ∫ 0 π ∫ 0 a 2 r 2 cos ⁡ θ + r 2 sen ⁡ θ d r d θ

Passo 4

Resolvendo a integral “de dentro”, temos que:

∫ 0 a 2 r 2 cos ⁡ θ + r 2 sen ⁡ θ d r = 2 r 3 3 cos ⁡ θ + r 3 3 sen ⁡ θ 0 a

Vamos aplicar os limites de integração:

2 a 3 3 cos ⁡ θ + a 3 3 sen ⁡ θ =   a 3 3 2 cos ⁡ θ + sen ⁡ θ

Agora que finalizamos a integral de “dentro”, vamos dar sequencia com a integral de “fora”.

Logo:

∫ 0 π ∫ 0 a 2 r 2 cos ⁡ θ + r 2 sen ⁡ θ d r d θ = ∫ 0 π a 3 3 2 cos ⁡ θ + sen ⁡ θ d θ

Resolvendo, agora, temos:

a 3 3 2 sen ⁡ θ - cos ⁡ θ 0 π

Vamos aplicar os limites de integração:

a 3 3 2 sen ⁡ π - cos ⁡ π - 2 sen ⁡ 0 + cos ⁡ 0   = a 3 3 ( 0 + 1 + 0 + 1 )

= 2 a 3 3

Portanto a nossa integral vale:

∫ 0 a ∫ - a 2 - y 2   a 2 - y 2   2 x + y d x d y = 2 a 3 3

Resposta

∫ 0 a ∫ - a 2 - y 2   a 2 - y 2   2 x + y d x d y = 2 a 3 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral iterada convertendo para coordenadas polares. ∫ 0 2 ∫ 0 4 - x 2e - x 2 - y 2 d y d x
Calcule a integral iterada convertendo para coordenadas polares. ∫ 0 1 / 2 ∫ 3 y 1 - y 2x y 2 d x d y
Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∫ R ∫ f x , y d A como uma integral iterada, onde f é uma arbitrária qualquer contínua em R .3.
Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∬ R f x ,yd A como uma integral iterada, onde f é uma arbitrária qualquer contínua em R .
29- Calcule a integral iterada, convertendo-a antes para coordenadas polares: ∫ 0 1 ∫ 0 1 - x 2 e x 2 + y 2 d y d x