Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.1 - Ex. 13

Calcule a integral dupla, identificando-a antes com o volume de um sólido.

∬ R   ( 4 - 2 y )   d A   ,                     R = 0 ,   1 × [ 0 ,   1 ]

Passo 1

Galera, pra gente calcular essa integral dupla, podemos interpretá-la como o volume acima do retângulo 0 ,   1 × 0 ,   1 e abaixo do plano z = 4 - 2 y , ou seja, a junção de um paralelepípedo com um cilindro triangular:

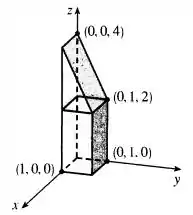
Passo 2

Então, pra calcular o volume do sólido, é só somar a área do paralelepípedo com a área do cilindro triangular:

∬ R   ( 4 - 2 y )   d A = 1   .   1   .   2 + 2   .   1 2 1 = 3

Resposta

∬ R   ( 4 - 2 y )   d A = 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral dupla.∬_R^() (x y^2)/(x^2 + 1) d A , R = {(x , y)| 0 = x = 1 , - 3 = y = 3 }
Calcule a integral dupla.∬_R^() cos ( x + 2 y ) d A , R = {(x , y)| 0 = x = pi , 0 = y = pi // 2 }
Calcule a integral dupla.∬_R^() x s e n ( x + y ) d A , R = [0 , (pi)/(6)] xx [0 , (pi)/(3)]
Calcule a integral dupla.∬_R^() x y e^(x^2 y) d A , R = [0 , 1] xx [ 0 , 2 ]
Calcule a integral dupla.∬_R^() (x)/(x^2 + y^2) d A , R = [1 , 2] xx [ 0 , 1 ]