Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.8 - Ex. 9

9. Em determinados intervalos para r , as equações de Lorenz exibem uma propriedade de duplicação do período semelhante ao que ocorre na equação de diferenças logística discutida na Seção 2.9. Cálculos cuidadosos podem revelar esse fenômeno.

(a) Um intervalo de duplicação do período inclui o valor r   =   100 . Seja r   =   100 e faça o gráfico da trajetória que começa em ( 5 ,   5 ,   5 ) ou em outro ponto inicial de sua escolha. A solução parece ser periódica? Qual é o período?

(b) Repita os cálculos do item (a) para valores ligeiramente menores de r. Quando r   ≅   99,98 , você pode ser capaz de observar que o período da solução dobra. Tente observar esse resultado fazendo cálculos para valores próximos de   r .

(c) Quando r diminui mais, o período da solução dobra repetidamente. O próximo valor de r para o qual o período dobra é em torno de r   =   99,629 . Tente observar isto traçando trajetórias para valores próximos de r .

Passo 1

L e t r a   A :

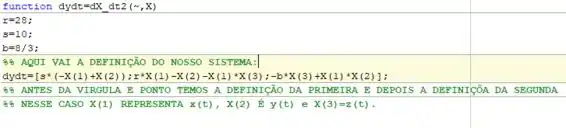
Novamente aqui, assim como os outros exercícios, temos que utilizar os códigos que desenvolvemos no exercício 6 para a solução numérica desse problema. A diferença é que aqui vamos considerar r = 100 , e um intervalo pequeno de variação do tempo, digamos t : 0 ,   3 , justamente para observamos mais de perto a periodicidade.

Vou colocar pra você aqui então um lembrete de como ficou o nosso código:

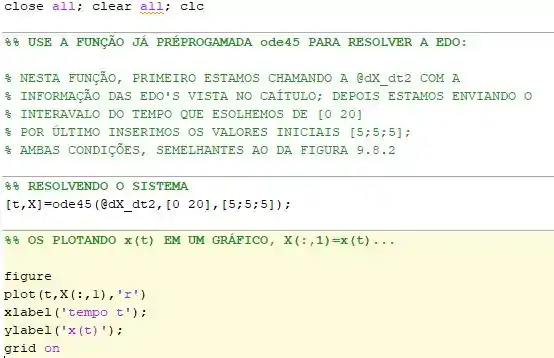
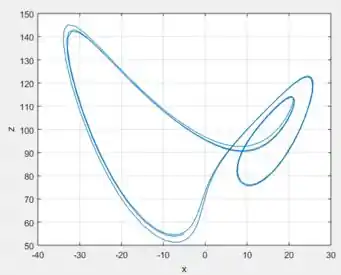
Mudando o r para 100 , e escolhendo outro ponto, digamos - 5 ,   - 13 ,   - 55 e plotando o gráfico no MatLab, obterá algo mais ou menos assim:

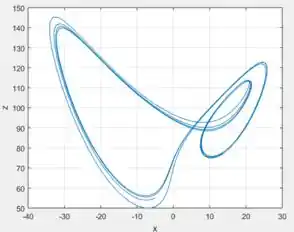
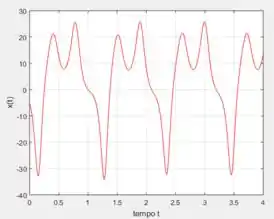
Perceba que foi plotado tanto o gráfico de x t por t quanto o, o gráfico da projeção no plano z x , em cima.

O período o período parece ser T = 1.1 .

Passo 2

L e t r a   B :

Aqui vamos mudar o r para um valor abaixo e pequeno e ver o que acontece com os gráficos, shall we?

  • Para r = 99.94 :

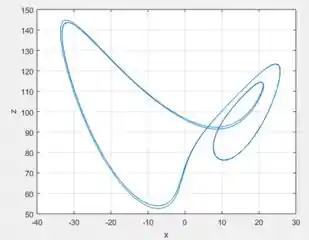
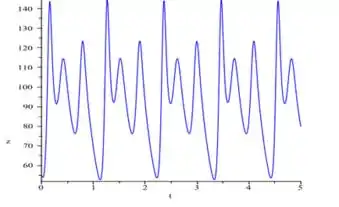
    • Observe no primeiro gráfico que as linhas meio que se duplicam, indicando que de fato há uma duplicação de período T . Embora essa duplicidade é sutil então não conseguimos perceber facilmente no gráfico de baixo. Mas, uma observação mais cuidadosa revela que o z t é levemente maior no segundo padrão.

  • Para r = 99.7 :

Passo 3

L e t r a   C :

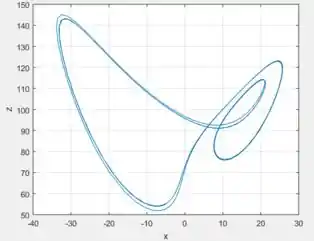
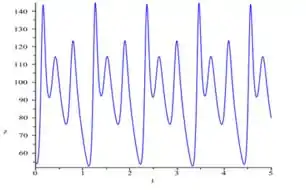
Desenhando agora os mesmo gráficos, mas para r = 99.5 ...

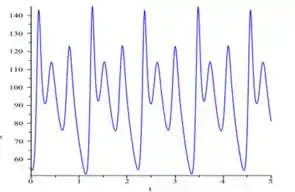
Observe que a segunda linha está cada vez mais evidente, mostrando que de fato se há dobro do período T . Nesse segundo gráfico também dá pra ver certo padrão que indica que o período saiu de T = 1.1 e foi para 2.2 :

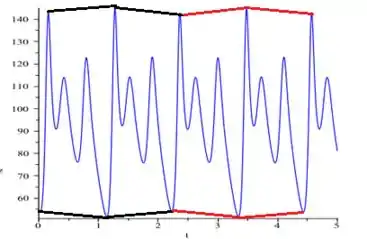
Viu só! O segmento preto ou o vermelho é um período .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a solução do sistema (2) ilustrada na Figura 9.5.3, estime o período o melhor possível. O resultado é o mesmo que para a aproximação linear?
Considere o sistemaem que a, σ, α, c e γ são constantes positivas. . Mostre que existe um valor de σ entre zero e aγ/c onde o ponto crítico no interior do primeiro quadrante muda de um ponto espiral p
Neste problema, vamos examinar a diferença de fase entre as variações cíclicas das populações de predadores e de presas dadas pelas Eqs. (24) desta seção. Vamos supor que K0 e que o tempo t é medido a
Considere o sistemaem que σ0. Note que esse sistema é uma modificação do sistema (2) no Exemplo 1.Determine o tipo e as propriedades de estabilidade de cada ponto crítico. Encontre o valor σ1
Encontre a razão entre as amplitudes das oscilações das populações de presas e de predadores em torno do ponto crítico (c/γ, a/α) usando a aproximação (24), válida para oscilações pequenas. Observe qu