Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.8 - Ex. 10

10. Considere, agora, valores de r ligeiramente maiores do que os no Problema 9.

(a) Faça o gráfico de trajetórias das equações de Lorenz para valores de r entre 100 e 100,78 . Você deveria observar uma solução periódica regular para esse intervalo de valores de r.

(b) Faça o gráfico de trajetórias das equações de Lorenz para valores de r entre 100,78 e 100,8 . Determine, o melhor que puder, como e quando a trajetória periódica deixa de existir.

Passo 1

L e t r a   A :

Novamente aqui, assim como os outros exercícios, temos que utilizar os códigos que desenvolvemos no exercício 6 para a solução numérica desse problema. A diferença é que aqui vamos considerar r entre 100 e 100,78 , e um intervalo pequeno de variação do tempo, digamos t : 0 ,   3 , justamente para observamos mais de perto a periodicidade.

Começando com r = 100.5 e o ponto inicial - 5 ,   - 13 ,   55 , e desenhando os gráficos tanto de z t em função de t quanto da projeção no plano x z , como fizemos nos exercícios anteriores...

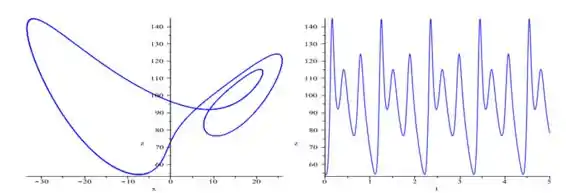
E agora para r = 100.7 ...

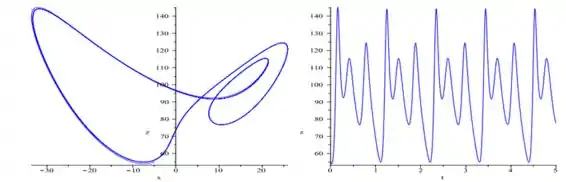
Obser que de fato é uma regularidade na resposta e vemos que ela é bem periódica mesmo.

Passo 2

L e t r a   B :

Considerando o mesmo ponto inicial, ou seja - 5 ,   - 13 ,   55 , só que agora colocando r = 100.80 e desenhando ambos gráficos desenhados acima...

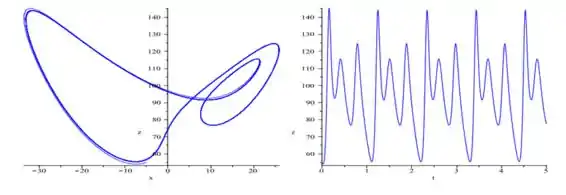
Considerando agora r = 100.81 ...

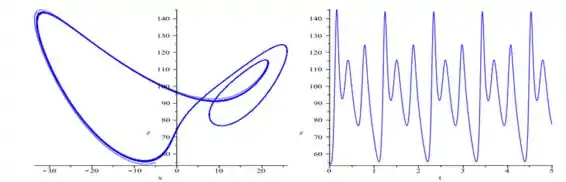
Agora para r = 100.82 ...

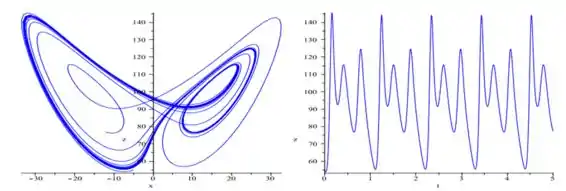
Para r = 100.83 ...

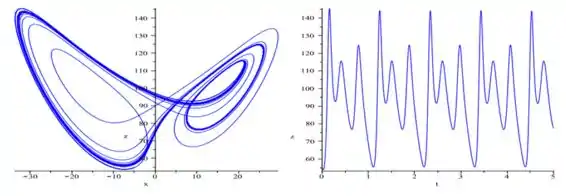
Para r = 100.84 ...

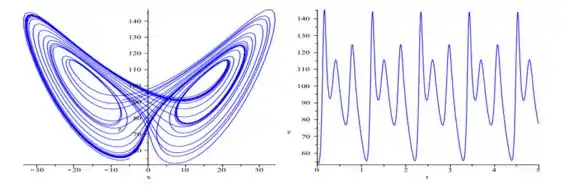
Observe que a partir do r = 100.81 as linhas de periodicidade começam a se separar de modo que quando r = 100.84 já a periodicidade nem existe mais.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Neste problema, vamos examinar a diferença de fase entre as variações cíclicas das populações de predadores e de presas dadas pelas Eqs. (24) desta seção. Vamos supor que K0 e que o tempo t é medido a
Considere o sistemaem que a e b são constantes positivas. Observe que esse sistema é o mesmo que o sistema do exemplo no texto quando a = 1 e b = 0,75. Suponha que as condições iniciais são x(0) = 5 e
Considere o sistemaem que a e b são constantes positivas. Observe que esse sistema é o mesmo que o sistema do exemplo no texto quando a = 1 e b = 0,75. Suponha que as condições iniciais são x(0) = 5 e
Considere o sistemaem que a, σ, α, c e γ são constantes positivas. . Determine a natureza e as propriedades de estabilidade de cada ponto crítico.
Considere o sistemaem que a e b são constantes positivas. Observe que esse sistema é o mesmo que o sistema do exemplo no texto quando a = 1 e b = 0,75. Suponha que as condições iniciais são x(0) = 5 e