Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.9 - Ex. 26

Determinar a massa do sólido acima do plano X Y , delimitado pelo cone 9 x 2 + z 2 = y 2 e o plano y = 9 . A densidade no ponto P ( x , y , z ) é proporcional à distância do ponto ao plano X Y .

Passo 1

O sólido está representado na figura abaixo:

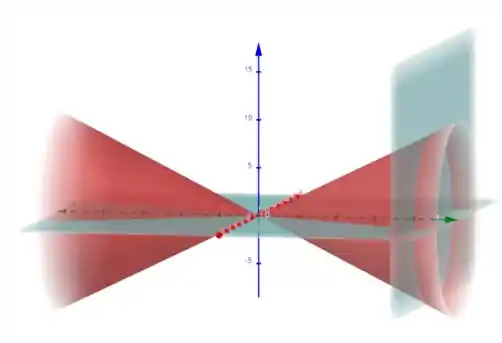
A densidade é dada por: δ x , y , z = z k , e podemos escrever a integral para a massa assim:

M = 2 k ∫ 0 9 ∫ 0 y 3 ∫ 0 y 2 - 9 x 2 z   d z d x d y

Passo 2

Calculamos agora:

M = 2 k   ∫ 0 9 ∫ 0 y 3 z 2 2 0 y 2 - 9 x 2 d x d y

M = 2 k ∫ 0 9 ∫ 0 y 3 y 2 - 9 x 2 d x d y

M = 2 9 k ∫ 0 9 y 3   d y

M = 2 9 k y 4 4 0 9

M = 2 k 9 ∙ 9 4 4

M = 729 k 2   u . m

Pronto! Essa é a massa procurada😉

Resposta

M = 729 k 2   u . m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Centro de massa e momento de inercia: repita o exercício 19 para δ x , y = 3 x 2 + 1
Encontrando o centro de massa: encontre o centro de massa de uma placa triangular fina delimitada pelo eixo y e as retas y = x e y = 2 - x se δ x , y = 6 x + 3 y + 3
Encontrando um centro de massa e momento de inércia: encontre o centro de massa e o momento de inercia em relação ao eixo y de uma placa retangular fina cortada no primeiro quadrante pelas retas x = 6
Encontrando o momento de inercia: encontre o momento de inercia em relação ao eixo x de uma placa fina de densidade δ = 1 delimitada pela circunferência x 2 + y 2 = 4 . Em seguida, utilize seu resulta
Encontrando a massa: encontre a massa de uma placa fina ocupando a região menor cortada pela elipse x 2 + 4 y 2 = 12 pela parábola x = 4 y 2 se δ x , y = 5 x