Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.9 - Ex. 20b
Calcular a massa dos sólidos limitados pelas superfícies dadas, considerando a densidade de massa igual a .
Passo 1
Vamos dar uma olhada na figura dessa região primeiro:
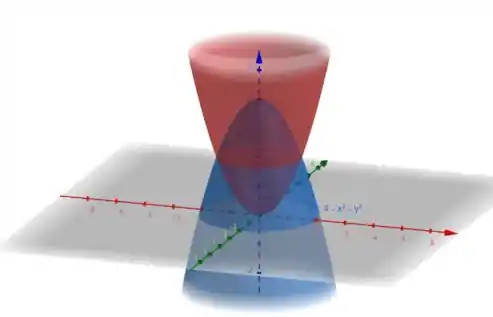
Sendo que a que está em azul é a função e a que está em vermelho é a .
Nós queremos da região roxa então (que limitada pelas duas).
Sabemos que a massa de um sólido é dada por:
Sendo que é a densidade. Vamos lá então...
Passo 2
Primeiro a gente vai fazer a interseção das duas funções:
Daqui a gente vê que a interseção é:
Ou seja, um círculo (ou um cilindro porque é no espaço) de raio .
Nesse caso a gente vai usar coordenadas cilíndricas. Vai ficar assim:
Sendo que e
Vemos que nesse caso e .
Passo 3
Vamos montar a integral da massa agora:
Agora a gente resolve:
Pronto! Essa é a massa procurada😉
Resposta
Exercícios de Livros Relacionados
Encontrando uma centroide: encontre a centeoide da região entre o eixo x e o arco y y = s e n x ,0 ≤ x ≤ π .
Encontrando um centroide: encontre o centroide da região no primeiro quadrante delimitado pelas reta x + y = 3
Encontrando um centro de massa: Encontre o centro de massa de uma placa fina de densidade δ = 3 delimitada pelas retas x = 0 , y = x e a parábola y = 2 - x 2 no primeiro quadrante.
Encontre o centro de massa e o momento de inercia em relação ao eixo x de uma placa fina delimitada pelas curvas x = y 2 x = 2 y - y 2 se a densidade no ponto (x,y) for δ x , y = y + 1 .
Encontrando um centroide: encontre o centroide da região cortado do primeiro quadrante pelo circulo x 2 + y 2 = a 2 .