Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.10 - Ex. 14a

Determinar os pontos de inflexão e reconhecer os intervalos onde a função seguinte tem concavidade voltada para cima ou para baixo.

Passo 1

Então meu amigo, vou te ajudar a resolver essa atividade hoje.

Veja vem, aqui queremos determinar os pontos de inflexão da função:

E também queremos encontrar os intervalos onde a função tem sua concavidade para cima e para baixo. Para isso devemos tomar conhecimento de que:

Se para todo em , então o gráfico de é concavo para cima em .
Se para todo em , então o gráfico de é concavo para baixo em .

Um ponto da curva é chamado de ponto de inflexão se é continua no ponto e a curva mudar de concava para cima para concava para baixo ou vice-versa em .

Passo 2

Vamos então calcular a segunda derivada.

Primeiro, calculamos a primeira derivada de :

Em seguida, calculamos a segunda derivada:

Passo 3

Para que o gráfico seja concavo para cima, deveremos ter , então vamos atrás desse intervalo:

Finalmente:

Então temos que nesse intervalo, a concavidade da função é para cima.

Agora vamos descobrir a concavidade para baixo. Para isso queremos:

Finalmente:

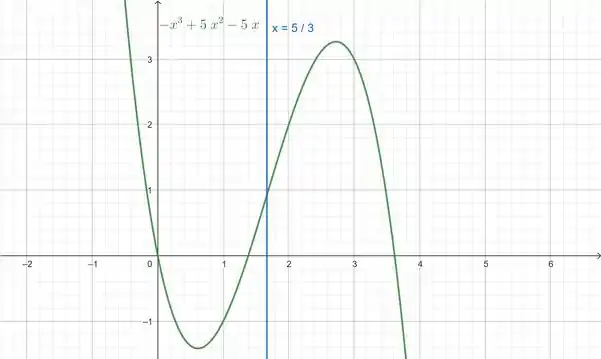
Onde a nossa concavidade agora é para baixo. Como a nossa concavidade muda no ponto , ele é um ponto de inflexão da nossa função.

Com o gráfico abaixo visualizamos o que fizemos:

Resposta

concavidade para baixo

concavidade para cima

ponto de inflexão

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

46. a) Mostre que e x ≥ 1 + x se x ≥ 0 .b) Mostre que e x ≥ 1 + x + 1 2 x 2 se x ≥ 0 .c) Confirme as desigualdades de a) e b) com algum recurso gráfico computacional.

53-54. Em cada parte, determine se a afirmação é verdadeira ou falsa. Se falsa, encontre funções para quais a afirmação não é válida.54. b) Se f e g forem côncavas para cima em um intervalo, então f .

45. a) Mostre que ln ⁡ x + 1 ≤ x se x ≥ 0 .b) Mostre que ln ⁡ x + 1 ≥ x - 1 2 x 2 se x ≥ 0 .c) Confirme as desigualdades em a) e b) com um recurso gráfico.

Uma tormenta que se aproxima provoca uma queda na temperatura. Apresente uma afirmação que indica que há um ponto de inflexão no gráfico da temperatura versus tempo. Explique como a existência de um p

Explique o que a análise de sinais de f ' x e f ' ' x revela sobre o gráfico de y = f x .