Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 6.6 - Ex. 28b
Determinar e representar graficamente um vetor normal a curva dada no ponto indicado:
b)
Passo 1
A ideia nessa questão é lembrar que o vetor gradiente é normal a curva. Então vamos montar uma expressão para e acharmos o gradiente de . Por fim, vamos verificar o valor do gradiente no ponto . A expressão que ele nos deu foi a seguinte:
Isto é,
Então a expressão para fica o seguinte:
Passo 2
Agora que já encontramos vamos ver como fica o gradiente de
Assim,
Derivando parcialmente, temos:
Passo 3
Para finalizarmos esse exercício, basta verificarmos o valor do gradiente no ponto , isto é, .
Fazendo as contas:
Representando geometricamente esse vetor:
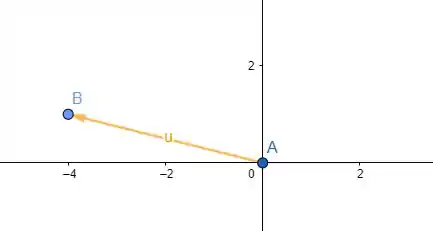
Resposta
Vetor:
Representação geométrica:
Exercícios de Livros Relacionados
Seja f x , y = 2 x 2 + 5 y 2 . Representar geometricamente ∇ f x 0 , y 0 , sendo x 0 ,y 0 dado por (1,1)
Nos exercícios 18 a 24, representar geometricamente o campo gradiente definido pela função dada: u x , y = 1 2 x 2 + y 2
Determinar e representar graficamente um vetor normal a curva dada no ponto indicado:c) x 2 + y 2 = 8 ; P 2 ,2
Provar as propriedades (a), (b) e (d) da Subseção 6.4.3.
Seja f x , y = 2 x 2 + 5 y 2 . Representar geometricamente ∇ f x 0 , y 0 , sendo x 0 ,y 0 dado por c) 1 2 ,3