Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 6.6 - Ex. 25c
Seja . Representar geometricamente , sendo dado por
c)
Passo 1
A ideia nesse exercício será encontrar o gradiente da função que ele nos deu usando aquela formula lá da teoria. Com isso, vamos verificar quem é e fazer sua representação geométrica. Vem comigo!
Passo 2
A expressão do é dada por:
Substituindo na expressão gradiente:
Derivando parcialmente, temos:
Passo 3
Para finalizar, vamos verificar como fica . Assim,
Fazendo as contas:
Com isso, vemos que representa o vetor . Fazendo uma ilustração:
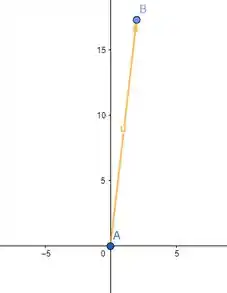
Resposta
Exercícios de Livros Relacionados
Em cerca de quanto g x , y , z = x + x c o sz - ys e nz + y irá variar se o ponto P(x, y, z) se mover de P0 (2,1,0) a uma distância de ds = 0,2 unidade na direção de P1(0,1,2)?
Variação de temperatura ao longo de uma curva espacial A temperatura em Celsius em uma região no espaço é dada por T(x, y, z) = 2x2 – xyz. Uma partícula está se movendo nessa região e sua posição no t
f x , y = x 2 + x y + y 2 ,P 0 - 1,1
f x , y = x 2 y + e x y sen y ,P 0 1 , 0
Nos Exercícios 7-10, encontre ∇ f no ponto dado. f x ,y ,z = 2 z 3 - 3 x 2 + y 2 z + tg - 1 x z , 1 ,1 ,1