Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.2 - Ex. 40

Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.

Cada curva integral do campo de direções

d y d x = 1 x 2 + 1

É o gráfico de uma função crescente de x .

Passo 1

Fala, pessoal! Esse exercício envolve a parte mais inicial sobre integrais indefinidas e, pra isso, vamos relembrar algumas definições.

Pelo Teorema no item 5.2 . 2 (na página 323 do livro CÁLCULO VOL. 1 - 10ª ED - ANTON), temos que a antiderivada, ou ainda, a integral indefinida de uma função f x em um intervalo aberto pode ser dada pela fórmula geral:

∫ f x d x = F x + C

Se

d d x F x = f x

Onde C é uma constante arbitrária. Portanto, para cada valor atribuído a essa constante, podemos conseguir uma função diferente, mas que também é a integral indefinida de f .

Então, para vermos o comportamento da função de x , temos que integrar a equação do campo de direções para saber qual é a cara dessa função.

Passo 2

Logo, fazendo a integração:

y = f x = ∫ 1 x 2 + 1 d x

Conseguimos resolver essa integral através de uma substituição simples e algumas manipulações futuras.

Então, considerando que x = t g u , tal que d x = sec 2 ⁡ u d u , temos:

∫ 1 x 2 + 1 d x = ∫ 1 t g 2 u + 1 sec 2 ⁡ u d u

Lembrando da identidade trigonométrica

1 + t g 2 u = sec 2 ⁡ u

Podemos substituir:

∫ 1 t g 2 u + 1 sec 2 ⁡ u d u = ∫ 1 sec 2 ⁡ u sec 2 ⁡ u d u = ∫ 1 sec ⁡ u sec 2 ⁡ u d u

Ou ainda:

∫ 1 sec ⁡ u sec 2 ⁡ u d u = ∫ sec ⁡ u d u

Passo 3

Se dermos uma olhada na Tabela 5.2 . 1 (página 324 do livro CÁLCULO VOL. 1 - 10ª ED - ANTON) não vamos conseguir encontrar uma fórmula definida para calcular essa última integral obtida, então precisamos encontrar uma forma para resolvê-la.

Uma ideia para esse caso é multiplicar o numerador e denominador por

sec ⁡ u + t g u

Tal que obtemos:

∫ sec ⁡ u sec ⁡ u + t g u sec ⁡ u + t g u d u = ∫ sec 2 ⁡ u + sec ⁡ u t g u sec ⁡ u + t g u d u

E podemos fazer uma outra substituição com:

v = sec ⁡ u + t g u → d v = sec ⁡ u t g u + sec 2 ⁡ u

Logo:

∫ sec 2 ⁡ u + sec ⁡ u t g u sec ⁡ u + t g u d u = ∫ d v v

Essa integral tem uma solução já definida e é dada por:

∫ d v v = ln ⁡ v + C

Assim, substituindo as variáveis originais de volta:

ln ⁡ v + C = ln ⁡ sec ⁡ u + t g u + C

Obs.: Nessa parte precisamos lembrar novamente da identidade trigonométrica

1 + t g 2 u = sec 2 ⁡ u → sec ⁡ u = 1 + t g 2 u

E da substituição aplicada

x = t g u

Logo:

= ln ⁡ 1 + t g 2 u + t g u + C = ln ⁡ 1 + x 2 + x + C

Passo 4

Dessa forma, visto que a função a ser analisada é:

f x = ln ⁡ 1 + x 2 + x + C

Podemos fazer o esboço do seu gráfico que está mostrado a seguir:

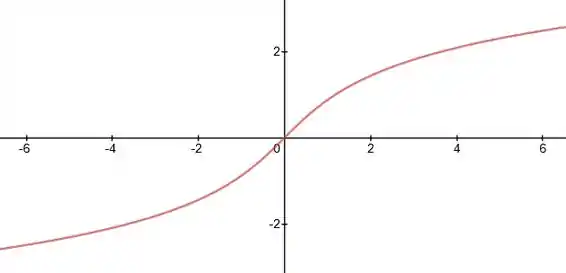
Observando esse esboço, claramente podemos ver que a função é crescente. A constante C irá apenas deslocar a curva para cima ou para baixo dependendo de seu valor e sinal, formando as diversas curvas integrais possíveis.

Logo, a afirmação é verdadeira.

Resposta

Verdadeiro

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral: ∫ 1 2 x 3 + 4 x d x
Calcule a integral: ∫ s e c ⁡ ( x ) t g x + c o s ⁡ ( x ) d x
Calcule a integral: ∫ 1 1 + x 2 + 2 1 - x 2 d x
Calcule a integral: ∫ 1 2 x x 2 - 1 + 1 - x 4 1 + x 2 d x
Calcule a integral: ∫ 4 s e n x + 2 c o s ⁡ ( x ) d x