Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.8 - Ex. 34
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.
Se for contínua em e , então converge.
Passo 1
Faaala aí, pessoal! Prontos pra mais um exercício com o Responde Aí?
Bom, para o caso do nosso exercício, precisamos lembrar parte da teria sobre as integrais impróprias.
Lembrando do Teorema (página do livro Cálculo Vol. - Ed. – ANTON), temos que uma integral imprópria de no intervalo é definida por:
No caso em que o limite existe, a integral converge para o valor desse limite.
Passo 2
Pelo limite dado no enunciado:
Colocando essa informação no gráfico da função , iremos ter algo parecido com:
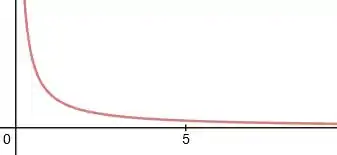
A curva irá apresentar uma assíntota horizontal quando cresce infinitamente.
Passo 3
Dessa forma, se formos analisar a área dessa curva, não poderemos calcular de forma direta, porque não conseguimos calcular uma área infinita. Para tanto, temos a maneira de fazer isso através do limite de uma integral dado pelo Teorema citado antes:
Como a função é contínua no intervalo dado, e a assíntota horizontal da curva dela converge para um valor inteiro, sendo uma constante inteira, a área pode ser limitada a uma área de valor inteiro e não infinito, como visto na segura abaixo (área sob a curva e limitada pelas linhas tracejadas):
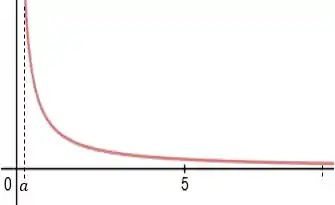
Portanto, a integral tem resultado inteiro e, por isso, é convergente.
Resposta
Verdadeiro