Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.8 - Ex. 42
Expresse a integral imprópria como um limite e, então, calcule esse limite com um CAS. Confirme sua resposta calculando diretamente as integrais com um CAS.
Passo 1
Vamos começar expressando a integral como limite:
Podemos usar a calculadora CAS do Geogebra para achar a antiderivada da função do integrando:
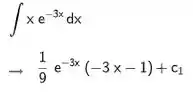
O nosso limite fica:
Usando a nossa calculadora CAS nele:
Passo 2
Usando direto nossa calculadora CAS para calcular a integral:
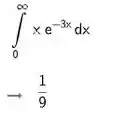
Deu o mesmo valor do nosso limite. A gente fez certinho! 😊
Resposta
Exercícios de Livros Relacionados
É convergente ou divergente? Justifique. ∫ 1 ∞ cos 2 x xd x
Suponha f integrável em a , t , para todo t≥ a , com f x ≥ 0 em [ a , + ∞ [ . Suponha que existem um a real e uma função g tais que, para todo x ≥ a , f x = 1 x a g x . Suponha além disso que l i m x
Suponha que f e f ' sejam de ordens exponencial γ 1 e γ 2 , respectivamente. Suponha, ainda, que f ' ' seja contínua. Verifique que ∫ 0 + ∞ e - s t f ' ' t d t = s 2 ∫ 0 + ∞ e - s t f t d t - s f 0 -
Seja f uma função, com derivada contínua, e de ordem exponencial γ . Verifique que, para sγ , ∫ 0 + ∞ e - s t f ' t d t é convergente e que ∫ 0 + ∞ e - s t f ' t d t = s ∫ 0 + ∞ e - s t f t d t - f 0
Procedendo como no exercício anterior, determine f tal que: f ' t - 2 f t = cos t e f 0 = 2 . f ' t + f t = e 2 t e f 0 = - 1 .