A tabela fornece a população dos Estados Unidos, em milhões, para os anos a.
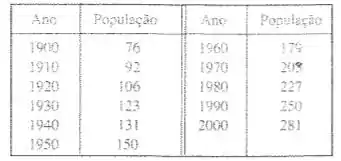
Use uma calculadora gráfica com capacidade para regressão exponencial para modelar a população do país desde . Utilize o modelo para estimar a população em 1925 e para predizer a população em e .
Passo 1
Eaee, belezinha??? Bom... o enunciado nos dá a seguinte tabela que mostra a população dos Estados Unidos, em milhões, no decorrer dos anos:
Queremos modelar uma função que represente a população do país desde 1990.
Para isso, utilizaremos uma calculadora gráfica com regressão exponencial. Mas o que é essa regressão???
Bom... Na regressão exponencial, o modelo assume a forma de uma função exponencial, geralmente da forma , onde:
- é a variável dependente;
- é a variável independente;
- é um parâmetro que representa o valor inicial da função;
- é um parâmetro que controla a taxa de crescimento ou decaimento da função;
- é a base do logaritmo natural, aproximadamente igual a .
Depois que conseguirmos essa função devemos estimar a população em 1925 e para predizer a população em e .
Agora bora lá!! 😉
Passo 2
Utilizaremos uma calculadora gráfica para representar os dados da tabela sob a forma de uma regressão exponencial.
Assim, jogando esses dados no Excel vamos obter:
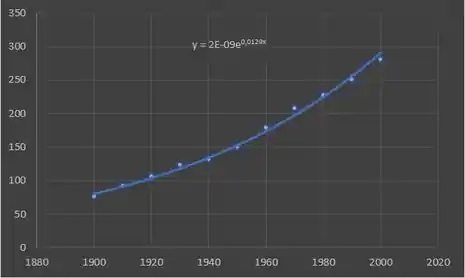
Note que a função modelada foi:
Estimando o valor da população para os anos de vamos obter
Entendeu direitinho?? Responde aee 😉