Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.4 - Ex. 63
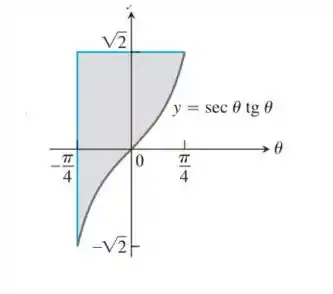
Determine a área da região sombreada.
Passo 1
Para determinar a área da região sombreada de podemos observar que a região delimitada entre possui uma área retangular acima do eixo e que a parte inferior ao eixo é complementar a área de um retângulo do intervalo . Assim podemos considerar dois retângulos com lados medindo e , e respectivamente. Logo a área total é obtida pela adição dos valores absolutos :
Resposta
Exercícios de Livros Relacionados
Calcule as integrais nos Exercícios 1-34.3. int_0^2 x ( x - 3 ) d x
Calcule as integrais nos Exercícios 1-34.21. int_(sqrt(2))^1 ((u^7)/(2) - (1)/(u^5)) d u
Calcule as integrais nos Exercícios 1-34.23. ∫ 1 2 ( s 2 + s ) s ² d s ²
Calcule as integrais nos Exercícios 1-34.17. int_0^((pi)/(8)) s e n 2 x d x
Calcule as integrais nos Exercícios 1-34.19. ∫ 1 - 1 ( r + 1 ) ² d r ²