Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.Revisão - Ex. 82
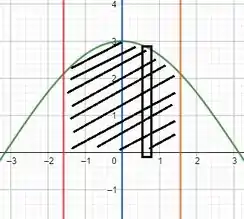
Nos Exercícios de 81 a 88, ache a área da região limitada pelas curvas e retas dadas. Faça uma figura mostrando a região e um elemento retangular da área. Expresse a medida da área como o limite de uma soma de Riemann e depois com a notação de integral definida. Calcule a integral pelo segundo teorema fundamental do Cálculo.
82) eixo x; ; .
Passo 1
Integrando e substituindo os limites:
Passo 2
A região limitada pelas curvas e retas fornecidas é a região hachurada abaixo:
Resposta
Exercícios de Livros Relacionados
Encontre a área da região sob a curva dada de 1 até 2 . y = 1 x 3 + x
Esboce a região no plano xy definida pelas inequações x - 2 y 2 ≥ 0 ,1 - x - y ≥ 0 e encontre sua área.
Use a Regra do Ponto Médio com n = 4 para aproximar a área de uma região limitada pelas curvas dadas. y = s e n 2 π x / 4 , y = cos 2 π x / 4 ,0 ≤ x ≤ 1
As larguras (em metros) de uma piscina com o formato de rim foram medidas a intervalos de 2 metros, como indicado na figura. Use a regra do ponto médio para estimar a área da piscina.
Use um gráfico para encontrar os valores aproximados das coordenadas x dos pontos de intersecção das curvas indicadas. A seguir, encontre a área aproximada da região delimitada pelas curvas. y = x cos