Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.6 - Ex. 83
Determine as áreas das regiões compreendidas entre as curvas nos Exercícios 81-84.
83.
Passo 1
Inicialmente, o que precisamos fazer é plotar esses gráficos para determinarmos as regiões compreendidas entre eles, ok? Se plotarmos os gráficos, teremos:
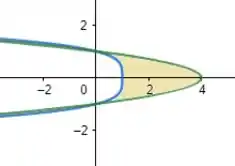
No qual a função em verde é e a função em azul é . Para o valor dessa área ser possível, teremos que integrar em , galera! Se integrarmos em , o problema ficará muito complicado.
Assim como discutido na seção 6 do George, os intervalos de integração para uma são , que são intervalos verticais (em ), não mais horizontais (em ). Além disso, temos que descobrir os pontos em que as funções se encontram para descobrirmos nosso intervalo de integração, beleza? Sabendo dessas informações, nosso problema fica bem mais tranquilo! Então bora lá!
Passo 2
Igualando as funções para descobrirmos seus pontos de encontro, teremos:
E aí, como descobrimos as raízes dessa função? Então, assim como visto lááá no ensino médio (algo difícil de lembrar mesmo), essa equação se trata de uma biquadrada. Para resolvermos isso aí, utilizamos a substituição . Se utilizarmos essa substituição, teremos:
Descobrindo as raízes, teremos:
Passo 3
Agora que descobrimos as duas raízes de , basta utilizarmos a substituição para descobrirmos as 2 raízes restantes em , se liga:
Para , temos:
Para , temos:
Agora que encontramos as 4 raízes de , podemos reescrever a nossa equação da seguinte forma:
Passo 4
Para calcularmos a área de uma região em relação à , assim como discutido na seção 6 do George, o que precisamos descobrir é quais são as curvas à direita e à esquerda. Depois de descoberto isso, basta fazermos:
Onde, nesse caso, seria a curva à direita e seria a curva à esquerda.
Se observarmos o gráfico, a função mais à direita é e a função mais à esquerda é . Algo que deve ser mencionado antes de escrevermos nossa integral é que o intervalo só vai de , isto é, não utilizaremos os pontos porque eles não satisfazem a condição de , beleza? Sendo assim, escrevendo nossa integral, teremos:
Para resolvermos essa integral precisaremos utilizar a seguinte regra:
Então: