Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.6 - Ex. 73
Determine as áreas das regiões compreendidas entre as retas e as curvas nos Exercícios 73-80.
73.
Passo 1
Inicialmente, o que precisamos fazer é plotar esses gráficos para determinarmos as regiões compreendidas entre eles, ok? Se plotarmos os gráficos, teremos:
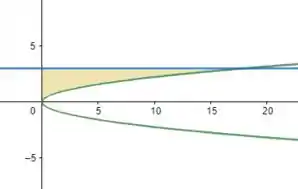
No qual a função em verde é e a função em azul é . Assim como discutido na seção 6 do George, os intervalos de integração para uma são , que são intervalos verticais (em ), não mais horizontais (em ). Sabendo dessas informações, nosso problema fica bem mais tranquilo! Então bora lá!
Passo 2
Para calcularmos a área de uma região em relação à , assim como discutido na seção 6 do George, o que precisamos descobrir é quais são as curvas à direita e à esquerda. Depois de descoberto isso, basta fazermos:
Onde, nesse caso, seria a curva à direita e seria a curva à esquerda.
Aplicando esse raciocínio, teremos:
Para resolvermos essa integral precisaremos utilizar a seguinte regra:
Então: