Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.6 - Ex. 48

Determine as áreas totais das regiões sombreadas

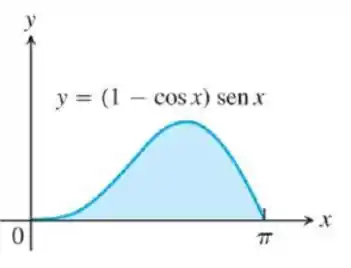
Passo 1

Precisamos determinar a área dada em azul na figura da questão. Desta forma, se f (x) >= g ( x ) ao longo de um intervalo [a , b] , então a área entre as curvas f ( x ) e g ( x ) é dada por:

A = int_a^b [f (x) - g (x)] d x

Desta forma, temos que identificar em cada caso quem é f ( x ) , g ( x ) e o intervalo [a , b] .

Passo 2

Vamos começar por montar qual a integral que devemos calcular. A área que devemos calcular é entre a função f (x) = ( 1 - cos x ) sen x e g ( x ) = 0 . O intervalo de integração é [0 , pi] . Como a função f (x) >= g ( x ) para todo x pertencente ao intervalo de integração, a área da região em azul é dada por:

A = int_0^(pi) ( 1 - cos x ) sen x d x

Passo 3

Agora que definimos a integral para calcular a área da região, vamos resolvê-la. Para isto, vamos fazer uma mudança de variáveis. Se u = 1 - cos x , d u = sen x d x . Modificando também os limites de integração, quando x = pi ⟹ u = 2 , já quando x = 0 ⟹ u = 0 . Desta forma, temos:

A = int_0^(pi) ( 1 - cos x ) sen x d x = int_0^2 u d u

A = int_0^2 u d u = ([(1)/(2) u^2]|_0^2

A = (1)/(2) * 2^2 - 0

A = 2

Resposta

A = 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

33. Determine o centroide de uma placa fina e plana que abrange a região compreendida pelas parábolas y = 2 x 2 e y = 3 - x 2 .
35. Determine o centroide de uma placa fina e plana que abrange a região "triangular" no primeiro quadrante, limitada pelo eixo y , pela parábola y = x 2 / 4 e pela reta y = 4 .
Desenhe a curva dada (coordenadas polares ). i ) rho = 2 - cos theta
Desenhe a curva dada (coordenadas polares ). g ) rho = cos 3 theta
Desenhe a curva dada (coordenadas polares ). o ) ρ = cos 2 ⁡ θ