Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 1i
Desenhe a curva dada (coordenadas polares ).
Passo 1
Nesse caso, podemos avaliar que:
Então sabemos agora que o raio vai variar entre 3 e 1.
Passo 2
Montando a tabela:
Como todos os valores de então não temos inversão da direção nem nada.
Passo 3
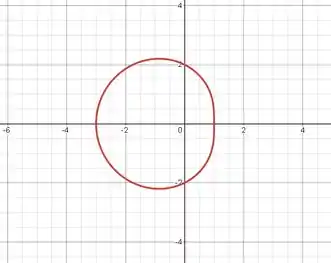
Resposta
Exercícios de Livros Relacionados
Ache a área da região limitada pela curva: y = 9 9 - x 2 pelos eixos coordenados e pela reta x = 2 2 .
Calcule a área da região situada no 1 ° quadrante, limitada acima pela curva x 4 - y 4 = 2 x y (coordenadas cartesianas) e abaixo por ρ 2 = 2 sen 2 θ (coordenadas polares), com ρ ≥ 0 .
Calcule a área do conjunto de todos os pontos θ , ρ tais que θ 2 ≤ ρ ≤ θ (coordenadas polares).
Passe a curva dada para coordenadas polares e desenhe-a. x 2 + y 2 3 2 = y 2
Sejam F 1 e F 2 dois pontos distintos do plano e seja k a metade da distância de F 1 a F 2 . O lugar geométrico dos pontos P do plano tais que P F 1 - ⋅ P F 2 - = k 2 denomina-se lemniscata de focos F