Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 1o
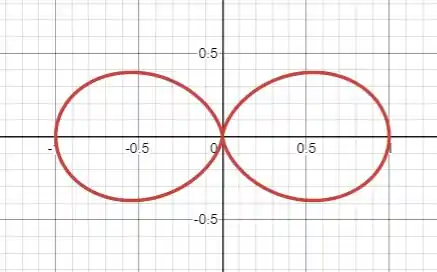
Desenhe a curva dada (coordenadas polares ).
Passo 1
Para essa equação vemos que , já que .
Por consequência disso, podemos imaginar que no intervalo vamos ter por duas vezes e também por três vezes.
Passo 2
Pela Tabela:
Passo 3
Quando você ligar os pontos vai ter um desenho assim:
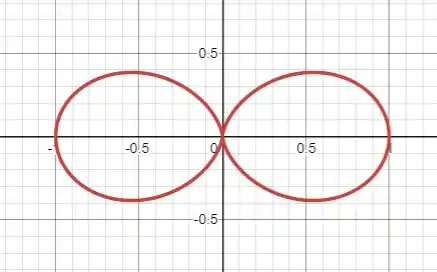
Resposta
Exercícios de Livros Relacionados
Nos Exercícios de 81 a 88, ache a área da região limitada pelas curvas e retas dadas. Faça uma figura mostrando a região e um elemento retangular da área. Expresse a medida da área como o limite de um
Nos Exercícios de 81 a 88, ache a área da região limitada pelas curvas e retas dadas. Faça uma figura mostrando a região e um elemento retangular da área. Expresse a medida da área como o limite de um
Ache a área da região limitada pelas curvas x = y^2 e x = y^3 .
Nos Exercícios de 81 a 88, ache a área da região limitada pelas curvas e retas dadas. Faça uma figura mostrando a região e um elemento retangular da área. Expresse a medida da área como o limite de um
92) Ache a área da região limitada pelo laço da curvas y 2 = x 2 . ( 4 - x ) .