Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 7.8 - Ex. 16
Determine se cada integral é convergente ou divergente. Calcule a convergente
Passo 1
Fala aí! Tudo bom?! Bora resolver uma integralzinha! Aqui temos:
O enunciado pede pra a gente determinar se essa integral é convergente ou divergente e se ela for convergente temos que calcula-la!
Podemos reescrever a nossa integral da seguinte forma:
Ficamos então com duas integrais impróprias do tipo 1, ou seja, com intervalo infinito. Por definição temos que:
Então vamos precisar calcular:
E depois avaliar seus limites! Se os dois limites existirem, então a integral é convergente!
Passo 2
Vamos calcular:
E depois aplicamos os limites de integração!
Aqui vamos usar a Substituição Simples, fazendo:
Substituindo:
Resolvendo a integral:
Passo 3
Sabendo que:
Temos que:
Além disso:
Passo 4
Agora vamos avaliar os limites:
Vamos pensar na função seno, se a gente olhar seu gráfico ele é assim:
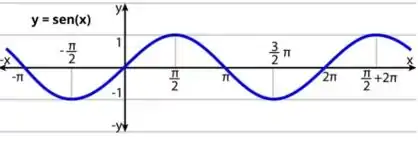
Então a medida que eu vou substituindo valores altos positivos ou negativos em uma função seno, ela não muda, ela sempre tem esse comportamento!
Isso significa que no infinito, ou menos infinito o seno não converge pra nenhum valor específico.
Portanto a nossa integral é divergente!
Resposta
iverge