Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.6 - Ex. 2b

Determine o centro de massa do gráfico da função dada.

f x = x 2 ,     - 1 2 ≤ x ≤ 1 2

Passo 1

Para encontrar o centro de massa ( x c , y c ) do gráfico de uma função no intervalo a , b usamos as fórmulas

x c = 1 L ∫ a b x 1 + f ' ( x ) 2   d x

y c = 1 L ∫ a b f x 1 + f ' ( x ) 2   d x

Onde L é o comprimento da função que é dado por

L = ∫ a b 1 + f ' ( x ) 2   d x

Neste caso o nosso intervalo é x ∈ - 1 2 , 1 2 .

Passo 2

Calculando primeiramente a derivada da função

f ' x = 2 x

E agora calculando o comprimento

L = ∫ - 1 / 2 1 / 2 1 + 4 x 2   d x

Aplicando a substituição trigonométrica

2 x = tg ⁡ u ⇒ 4 x 2 = tg 2 ⁡ u 2   d x = sec 2 ⁡ u d u ⇒ d x = sec 2 ⁡ u d u 2

Esquecendo dos limites de integração por enquanto

∫ 1 + 4 x 2   d x = ∫ 1 + tg 2 ⁡ u sec 2 ⁡ u d u 2

= 1 2 ∫ sec 3 ⁡ u d u = 1 2 ∫ 1 cos 3 ⁡ u d u

Multiplicando por 1 , mas com uma cara diferente

= 1 2 ∫ cos ⁡ u cos 4 ⁡ u d u = 1 2 ∫ cos ⁡ u cos 2 ⁡ u 2 d u

= 1 2 ∫ cos ⁡ u 1 - sen 2 ⁡ u 2 d u

Fazendo a substituição

w = sen ⁡ u d w = cos ⁡ u d u

1 2 ∫ cos ⁡ u 1 - sen 2 ⁡ u 2 d u = 1 2 ∫ 1 1 - w 2 2   d w

Focando no integrando

1 1 - w 2 2 = 1 1 - w 1 + w 2

Podemos expandir a fração da seguinte forma

1 1 - w 2 2 = A 1 - w + B 1 - w 2 + C 1 + w + D 1 + w 2

A 1 - w 2 1 + w + B 1 + w 2 + C 1 - w 2 1 - w + D 1 - w 2 = 1

A 1 + w - w 2 - w 3 + B 1 + 2 w + w 2 + C 1 - w - w 2 + w 3 + D 1 - 2 w + w 2 = 1

E tiramos o sistema

A + B + C + D = 1 A + 2 B - C - 2 D = 0 - A + B - C + D = 0 - A + C = 0

Da última equação tiramos

A = C

Fazendo a diferença das equações

A + B + C + D = 1 - A + B - C + D = 0

2 A + 2 C = 1

4 A = 1

A = C = 1 4

Utilizando A + 2 B - C - 2 D = 0 , como A = C

2 B - 2 D = 0

B = D

E podemos substituir na equação

- A + B - C + D = 0

2 B = 2 A

B = A

B = D = 1 4

E temos

1 1 - w 2 2 = 1 4 1 1 - w + 1 1 - w 2 + 1 1 + w + 1 1 + w 2

Na integral

1 2 ∫ 1 1 - w 2 2   d w = 1 8 ∫ 1 1 - w d w + ∫ 1 1 - w 2 d w + ∫ 1 1 + w d w + ∫ 1 1 + w 2 d w

= 1 8 - ln ⁡ 1 - w + 1 1 - w + ln ⁡ 1 + w - 1 1 + w + C

= 1 8 2 w 1 - w 2 + ln ⁡ 1 + w 1 - w + C

Retornando as variáveis

1 2 ∫ sec 3 ⁡ u d u = 1 8 2 sen ⁡ u 1 - sen 2 ⁡ u + ln ⁡ 1 + sen ⁡ u 1 - sen ⁡ u + C

= 1 8 2 sen ⁡ u cos 2 ⁡ u + ln ⁡ 1 + sen ⁡ u 1 - sen ⁡ u ⋅ 1 + sen ⁡ u 1 + sen ⁡ u + C

= 1 8 2 sen ⁡ u sec 2 ⁡ u + ln ⁡ 1 + sen ⁡ u 2 cos 2 ⁡ u + C

= 1 4 sen ⁡ u sec 2 ⁡ u + ln ⁡ 1 + sen ⁡ u cos ⁡ u + C

= 1 4 sen ⁡ u sec 2 ⁡ u + ln ⁡ sec ⁡ u + tg ⁡ u + C

Utilizando agora a relação 2 x = tg ⁡ u para montar o triângulo:

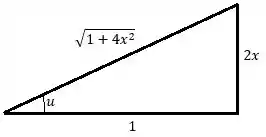
Temos então

∫ 1 + 4 x 2   d x = 1 4 2 x 1 + 4 x 2 1 + 4 x 2 + ln ⁡ 1 + 4 x 2 + 2 x + C

= 1 4 2 x 1 + 4 x 2 + ln ⁡ 1 + 4 x 2 + 2 x + C

Nos limites de integração

L = ∫ - 1 / 2 1 / 2 1 + 4 x 2   d x = 1 4 2 x 1 + 4 x 2 + ln ⁡ 1 + 4 x 2 + 2 x - 1 / 2 1 / 2

= 1 4 2 1 2 1 + 4 1 2 2 + ln ⁡ 1 + 4 1 2 2 + 2 1 2 - 1 4 - 2 1 2 1 + 4 - 1 2 2 + ln ⁡ 1 + 4 - 1 2 2 - 2 1 2

= 1 4 1 + 1 + ln ⁡ 1 + 1 + 1 - 1 4 - 1 + 1 + ln ⁡ 1 + 1 - 1

= 2 2 + 1 4 ln ⁡ 2 + 1 - 1 4 ln ⁡ 2 - 1

L = 2 2 + 1 4 ln ⁡ 2 + 1 2 - 1

Passo 3

Por fim calculamos as coordenadas do centro de massa

x c = 1 L ∫ - 1 / 2 1 / 2 x 1 + 4 x 2   d x

Como se trata de uma função ímpar em um intervalo simétrico

x c = 0

Passo 4

E a coordenada y c

y c = 1 L ∫ - 1 / 2 1 / 2 x 2 1 + 4 x 2   d x

Esquecendo os limites de integração por um instante, vamos calcular a integral por partes da seguinte forma

∫ f ⋅ g '   d t = f ⋅ g - ∫ f ' ⋅ g   d t

Neste caso nossas funções são

f = x g ' = x 1 + 4 x 2  

Para integrar g ' vamos usar a substituição

u = 1 + 4 x 2 d u = 8 x   d x ⇒ x   d x = d u 8

∫ x 1 + 4 x 2   d x = 1 8 ∫ u   d u

= 1 8 2 u 3 2 3 = u 3 12 = 1 + 4 x 2 3 12

E temos

f = x g ' = x 1 + 4 x 2 → f ' = 1 g = 1 + 4 x 2 3 12

∫ x 2 1 + 4 x 2   d x = x 1 + 4 x 2 3 12 - 1 12 ∫ 1 + 4 x 2 3 d x

Focando da segunda integral

∫ 1 + 4 x 2 3

Reutilizando a substituição

2 x = tg ⁡ u ⇒ 4 x 2 = tg 2 ⁡ u 2   d x = sec 2 ⁡ u d u ⇒ d x = sec 2 ⁡ u d u 2

∫ 1 + 4 x 2 3 = ∫ 1 + tg 2 ⁡ u 3 sec 2 ⁡ u d u 2

= 1 2 ∫ sec 5 ⁡ u d u

Calculamos a integral de sec 3 ⁡ u e em geral a integral de sec n ⁡ u com n um inteiro impar tem um método de solução parecido. Como a resolução está bem extensa e o método para resolver esta integral é repetitivo comparado ao da sec 3 ⁡ u , vamos usar uma propriedade que diz

∫ sec n ⁡ x d x = sec n - 1 ⁡ x sen ⁡ x n - 1 + n - 2 n - 1 ∫ sec n - 2 ⁡ x d x

Neste caso

∫ sec 5 ⁡ u d u = sec 4 ⁡ u sen ⁡ u 4 + 3 4 ∫ sec 3 ⁡ u d u

E a integral de sec 3 ⁡ u nós já calculamos

∫ sec 5 ⁡ u d u = sec 4 ⁡ u sen ⁡ u 4 + 3 8 sen ⁡ u sec 2 ⁡ u + ln ⁡ sec ⁡ u + tg ⁡ u

E temos

∫ 1 + 4 x 2 3 = 1 2 ∫ sec 5 ⁡ u d u

Retornando à variável x utilizando agora a relação 2 x = tg ⁡ u para montar o triângulo:

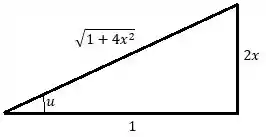
∫ 1 + 4 x 2 3 = 1 2 1 + 4 x 2 2 2 x 4 1 + 4 x 2 + 3 8 2 x 1 + 4 x 2 1 + 4 x 2 + ln ⁡ 1 + 4 x 2 + 2 x

= 1 4 x 1 + 4 x 2 1 + 4 x 2 + 3 8 x 1 + 4 x 2 + 3 16 ln ⁡ 1 + 4 x 2 + 2 x

E podemos afirmar que

∫ x 2 1 + 4 x 2   d x = x 1 + 4 x 2 3 12 - 1 12 ∫ 1 + 4 x 2 3 d x

∫ x 2 1 + 4 x 2   d x = x 1 + 4 x 2 3 12 - 1 12 1 4 x 1 + 4 x 2 1 + 4 x 2 + 3 8 x 1 + 4 x 2 + 3 16 ln ⁡ 1 + 4 x 2 + 2 x

= x 1 + 4 x 2 3 12 - 1 48 x 1 + 4 x 2 1 + 4 x 2 - 1 32 x 1 + 4 x 2 - 1 64 ln ⁡ 1 + 4 x 2 + 2 x

Nos limites de integração

y c = 1 L x 1 + 4 x 2 3 12 - 1 48 x 1 + 4 x 2 1 + 4 x 2 - 1 32 x 1 + 4 x 2 - 1 64 ln ⁡ 1 + 4 x 2 + 2 x - 1 / 2 1 / 2

Como se trata de uma função par

= 1 L 1 + 4 1 2 2 3 24 - 1 96 1 + 4 1 2 2 1 + 4 1 2 2 - 1 64 1 + 4 1 2 2 - 1 64 ln ⁡ 1 + 4 1 2 2 + 2 1 2 - 1 L - 1 + 4 - 1 2 2 3 24 + 1 96 1 + 4 - 1 2 2 1 + 4 - 1 2 2 + 1 64 1 + 4 - 1 2 2 - 1 64 ln ⁡ 1 + 4 - 1 2 2 - 2 1 2

= 1 L 2 2 24 - 1 96 2 2 - 1 64 2 - 1 64 ln ⁡ 2 + 1 - 1 L - 2 2 24 + 1 96 2 2 + 1 64 2 - 1 64 ln ⁡ 2 - 1

= 2 L 2 12 - 2 48 - 2 64 + 1 L - 1 64 ln ⁡ 2 + 1 + 1 64 ln ⁡ 2 - 1

= 2 L 16 - 4 - 3 2 192 + 1 64 L ln ⁡ 2 - 1 2 + 1

= 2 L 3 2 64 + 1 64 L ln ⁡ 2 - 1 2 + 1 = 6 2 + ln ⁡ 2 - 1 2 + 1 64 L

Por fim substituímos L

y c = 6 2 + ln ⁡ 2 - 1 2 + 1 64 2 2 + 1 4 ln ⁡ 2 + 1 2 - 1

y c = 6 2 + ln ⁡ 2 - 1 2 + 1 32 2 + 16 ln ⁡ 2 + 1 2 - 1

Resposta

x c = 0

y c = 6 2 + ln ⁡ 2 - 1 2 + 1 32 2 + 16 ln ⁡ 2 + 1 2 - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a área apresentada por g x . A seguir, encontre g ' x Utilizando a parte 1 do teorema fundamental do cálculo parte 1 Calculando a integral usando a parte 2, e então, derivando. g x = ∫ 0 x ( 2
Se f x = ∫ 0 x1 + t 2 d t e g x = ∫ 0 y f ( x ) d x , encontre g ' ' π 6 .
Se f 1 = 12 , f ' é contínua e ∫ 1 4f ' xd x = 17 . Qual o valor de f 4 ?
Em que intervalo a curva y = ∫ 0 x t 2 t 2 + t + 2d t é côncava para baixo?
Calcule a integral. ∫ - 1 1 t 1 - t 2d t