Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 2a
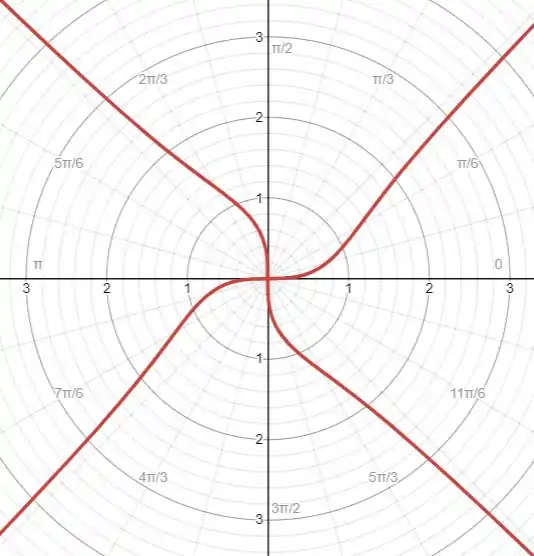
Passe a curva dada para coordenadas polares e desenhe-a.
Passo 1
Utilizando a substituição
Para transformar a equação para coordenadas polares
Utilizando a relação
Utilizando a diferença de quadrados , neste caso e
Pela identidade fundamental da trigonometria e usando a relação
Passo 2
A tangente é uma função problemática, pois não podemos aplicar um argumento múltiplo inteiro de , como temos , não podemos aplicar múltiplos de .
Nesses pontos, vamos calcular os limites laterais, para isso vamos assumir que , então temos os seguintes limites
Temos que
Logo
Para o outro lateral
E a tangente neste valor é negativa, então a função não assume valores reais
Montando a tabelinha de e , com os ângulos principais:
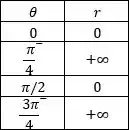
E esse padrão se repete.
Passo 3
Esboçando o gráfico no plano polar
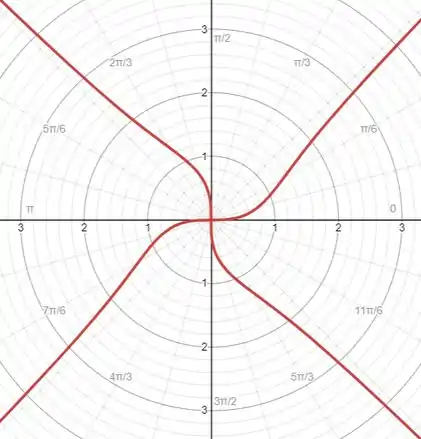
Resposta
