Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.3 - Ex. 6
Esboce a área apresentada por . A seguir, encontre
- Utilizando a parte 1 do teorema fundamental do cálculo parte 1
- Calculando a integral usando a parte 2, e então, derivando.
Passo 1
Sabendo que a área da função é o “espaço “entre o gráfico da função e a curva. Vamos esboçar!
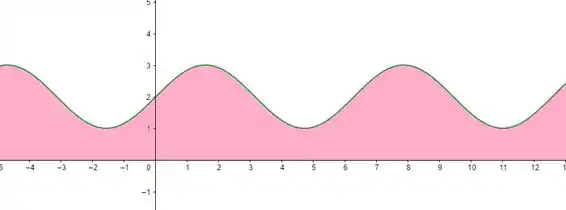
Passo 2
Agora vamos resolver a letra a)
Usando o teorema fundamental do cálculo,
Passo 3
Resolvendo item b)
Usando a regra da soma,
Ou seja,
Derivando,
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
A integral definida de f no intervalo [ a ,b ] está definida como o limite: ∫ a b f x d x = lim max ∆ x k → 0 ∑ k = 1 n f ( x k * ) ∆ x k Explique o significado dos vários símbolos do lado direito d
Em cada parte, use a informação do Exercício 27 para calcular a integral dada. Se não houver informação suficiente, então aponte isso. ∫ 0 1 f x d x = 1 2 ,∫ 1 2 f x d x = 1 4, ∫ 0 3 f x d x = - 1 ,∫
Dê um argumento geométrico para calcular: ∫ 0 1 2 x - 1 d x
Suponha que ∫ 0 1 f x d x = 1 2 ,∫ 1 2 f x d x = 1 4, ∫ 0 3 f x d x = - 1 ,∫ 0 1 g x d x = 2 Em cada parte, use essa informação para calcular a integral dada, se possível. Se não houver informações su
Em cada parte, calcule a integral. Quando apropriado, use uma fórmula geométrica. ∫ - 1 1 ( 1 + 1 - x 2 ) d x ∫ 0 3 ( x x 2 + 1 - 9 - x 2 ) d x ∫ 0 1 x 1 - x 4 d x