Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.6 - Ex. 1a

Determine o centro de massa da região A dada

a ) A = {(x , y) in R | 0 <= x <= 1 , 0 <= y <= x^3}

Passo 1

Para encotrarmos o centro de massa precisamos achar x_c e y_c que são descritos por:

x_c = (int_a^b x [g (x) - f (x)] d x)/(Á r e a d e A)

y_c = (1)/(2) (int_a^b [g (x) + f (x)] [g (x) - f (x)] d x)/(Á r e a d e A)

A figura fica assim:

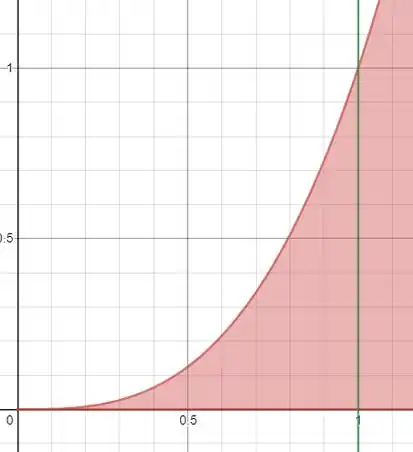
Limitada por 0 <= y <= x^3 e x = 1 .

Daí vemos que a Área de A vai ser igual:

Á r e a d e A = int_0^1 x^3 d x = [(x^4)/(4)] (1)/(0) = (1)/(4)

Ok! Agora que temos a Área de A vamos achar as integrais restantes:

Como g (x) = x^3 e f (x) é o próprio eixo x , podemos dizer que f (x) = 0 , daí:

int_a^b x [g (x) - f (x)] d x = int_0^1 x [x^3 - 0] d x = int_0^1 x^4 d x = [(x^5)/(5)] (1)/(0) = (1)/(5)

int_a^b [g (x) + f (x)] [g (x) - f (x)] d x = int_0^1 [x^3 + 0] [x^3 - 0] d x = int_0^1 x^6 d x = [(x^7)/(7)] (1)/(0) = (1)/(7)

Passo 2

Agora substituímos nas equações de x_c e y_c :

x_c = (int_a^b x [g (x) - f (x)] d x)/(Á r e a d e A) = ((1)/(5))/((1)/(4)) = (4)/(5)

y_c = (1)/(2) (int_a^b [g (x) + f (x)] [g (x) - f (x)] d x)/(Á r e a d e A) = ((1)/(2) xx (1)/(7))/((1)/(4)) = (2)/(7)

Resposta

(x_c , y_c) = ((4)/(5) , (2)/(7))

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Aplicar os resultados dos exercícios 9 e 10 para encontrar o menor e o maior valor possível da integral a seguir. ∫ - 1 4 ( x 4 - 8 x 2 + 16 ) d x
int_0^4 (2 x + 1)^(- (1)/(2)) d x
Aplicar os resultados dos exercícios 9 e 10 para encontrar o menor e o maior valor possível da integral a seguir. ∫ 1 4 | x - 1 | d x
int_(- 3)^(- 2) (t - (1)/(t))^2 d t
∫ - 1 1 x 2 d x x 3 + 9