Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.3 - Ex. 6
Determine o comprimento das curvas. Se tiver um programa gráfico, talvez queira esboçar o gráfico dessas curvas para ver como elas são
De a
Passo 1
Para calcularmos o comprimento da curva, devemos usar a fórmula para o comprimento.
Como temos uma função de , a fórmula vai ser:
Entao precisamos de duas coisas, o intervalo de intergração, que ele deu no enunciado, e a derivada, em , da , que é a função do enunciado.
O intervalo é de até , vamos para a derivada.
Primeiro, vamos escrever aque l como potência:
Derivando:
Passo 2
Vamos para a interal do comprimento agora, usando oque achamos:
Abrindo aquele quadrado:
Aquele termo dentro da raiz vai ser um trinômio quadrado perfeito
Po, temos que adivinhar isso sempre? Não, mas fica aqui a dica. Quando estamos nessas questões de comprimento de arco, é muito comum aparecer trinômios quadrados perfeitos dentro dessa raiz quadrada, então sempre procure esses safadinho. Para isso, tente sempre comparar com
O comprimento vai ser:
Como o termo dentro da raiz é positivo nesse intervalo da integral, podemos cortar a raiz com o quadrado e não colocar o módulo.
Passo 3
Vamos resolver essa integral:
Primeiro, vamos ver a integral indefinida:
Passo 4
Voltando para a nossa integral definida:
Passo 5
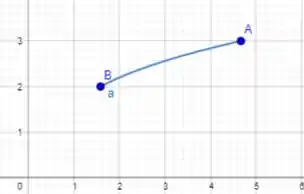
Segue o gráfico dessa função para enxergamos como ela é:
