Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.7 - Ex. 2c
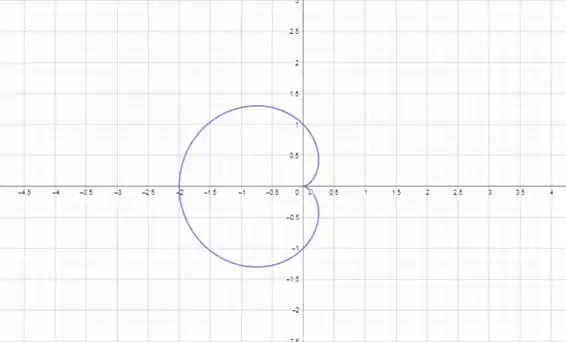
Passe a curva para coordenadas polares e desenhe-a:
x² + y² + x =
Passo 1
Sabemos que:
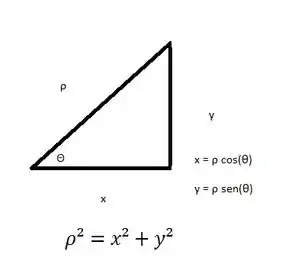
Logo:
X² + y² + x =
=
Igualando:
Simplificando:
1 =
Passo 2
Para esboçar o gráfico, precisamos de uma tabela de valores:
Passo 3
Agora basta ligar os pontos e desenhar a curva:
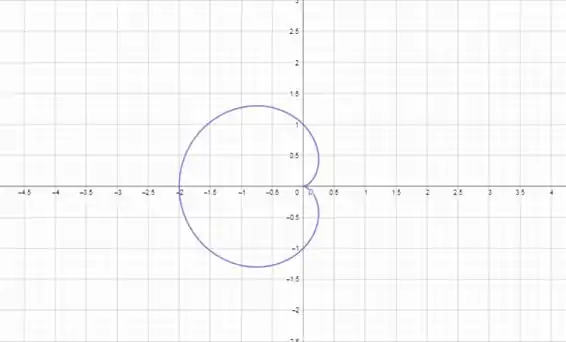
Resposta
Exercícios de Livros Relacionados
Se f x = ∫ 0 x cos td t , ache o comprimento do arco do gráfico de f do ponto onde x = π 3 ao ponto onde x = π 2 .
Nos exercícios de 23 a 26, use a regra de Simpson com n = 8 para aproximar até quatro casas decimais o comprimento de arco. (26) O arco da curva y = t g x , da origem ao ponto ( 1 4 π , 1 ) .
Nos exercícios de 23 a 26, use a regra de Simpson com n = 8 para aproximar até quatro casas decimais o comprimento de arco. (24) O arco da curva co-seno, da origem ao ponto ( π 3 , 1 2 ) .
Nos exercícios de 23 a 26, use a regra de Simpson com n = 8 para aproximar até quatro casas decimais o comprimento de arco. (23) O arco da curva seno, da origem ao ponto ( π ,0 ) .
Nos exercícios de 23 a 26, use a regra de Simpson com n = 8 para aproximar até quatro casas decimais o comprimento de arco. (25) O arco da curva y = x 3 3 , da origem ao ponto ( 1 , 1 3 ) .