Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios práticos - Ex. 20

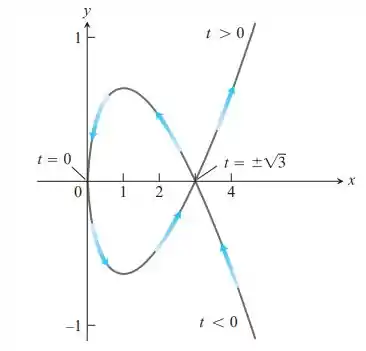
Determine o comprimento do laço delimitado x = t 2 ,   y = t 3 3 - t mostrado aqui. O laço começa em t = - 3 e termina em t = 3 .

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de equações paramétricas e coordenadas polares.

Vamos agora resolver os exercícios práticos sobre comprimentos de curvas.

Podemos determinar o comprimento da curva pedida utilizando:

L = ∫ t 1 t 2 d x d t 2 + d y d t 2 d t

Para isso, vamos derivar x em relação a t:

d x d t = 2 t

De modo que:

d x d t 2 = 2 t 2 = 4 t 2

De forma similar, vamos derivar y em relação a t:

d y d t = 3 t 2 3 - 1 = t 2 - 1

De modo que:

d y d t 2 = t 2 - 1 2 = t 4 - 2 t 2 + 1

Passo 2

Daí, temos que:

d x d t 2 + d y d t 2 = 4 t 2 + t 4 - 2 t 2 + 1 = t 4 + 2 t 2 + 1 = t 2 + 1 2 = t 2 + 1

Aplicando na equação do comprimento da curva, teremos que:

L = ∫ - 3 3 t 2 + 1 d t

Logo:

L = t 3 3 + t | - 3 3 = 3 3 3 + 3 - - 3 3 3 + - 3 =

= 3 3 3 + 3 - - 3 3 3 - 3 = 2 3 + 2 3 = 4 3

E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.

Resposta

4 3

Exercícios de Livros Relacionados

Use a Fórmula 2 para deduzir a Fórmula 7 a partir da Fórmula 8.2.5, no Volume 1, para o caso no qual a curva pode ser representada na forma y = F x ,a ≤ x ≤ b .
Encontre os comprimentos das curvas nos Exercícios 13-19. x = 5 cos ⁡ t - cos ⁡ 5 tey = 5 s e nt - s e n5 t ; 0 ≤ t ≤ π 2
Encontre os comprimentos das curvas nos Exercícios 13-19. y = x 1 / 2 - 1 3 x 3 / 2 ; 1 ≤ x ≤ 4
Encontre os comprimentos das curvas nos Exercícios 13-19. y = 5 12 x 6 / 5 - 5 8 x 4 / 5 ; 1 ≤ x ≤ 32