Determine as dimensões de uma lata cilíndrica, com tampa, com volume , de forma que sua área total seja mínima.

Certo, agora já temos uma expressão envolvendo e . Como queremos que a área total seja mínima, vamos montar uma expressão. Se liga nessa ilustração:

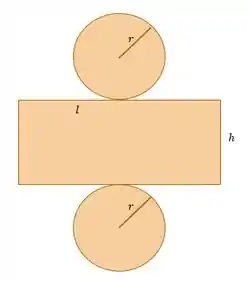
Repare que a largura será o comprimento da circunferência, isto é:

Então a área lateral fica o seguinte:

E para a área da tampa:

Portanto,

Para minimizar a , vamos colocar a expressão acima em função apenas de . Do passo 1:

Substituindo na expressão da área total:

Simplificando:

Agora vamos derivar e achar os pontos críticos, vem comigo!

Assim,

Para achar os pontos críticos, vamos igualar a zero:

Logo,

Isto é,

Opa, então já achamos o raio. Para o volume, vamos voltar na equação . Assim,

Portanto,