Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 34
Determine as dimensões do retângulo de maior área que pode ser inscrito em um semicírculo de raio 3. (Veja a figura a seguir.)
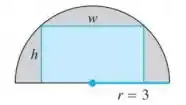
Passo 1
Em essência, este se trata de um problema no qual as noções de cálculo utilizadas para resolvê-lo são beeem tranquilas galera, se liga! Considerando apenas a parte positiva dos eixos, uma vez que o retângulo apresenta dimensões simétricas em relação ao eixo , isto é, o eixo divide o retângulo em duas partes iguais, temos que a equação que define a área do retângulo inscrito é:
Aqui vale ressaltar que se trata do tamanho da base do retângulo, tudo bem? Como é apenas metade do tamanho da base, então o tamanho inteiro é ! Mas o que seria esse ? Esse termo é a função que está delimitando o retângulo superiormente, galera! A função que delimita esse retângulo é a equação da circunferência, dada por:
Substituindo na equação da área, teremos:
Passo 2
O conceito necessário do cálculo que foi comentado lá no início se trata da noção de máximos e mínimos, pessoal. Para encontrar máximos e mínimos de uma função qualquer, igualamos a derivada da função a zero e assim descobrimos seus pontos críticos! Sim, é só isso! Derivando a função de área que encontramos e igualando a zero, teremos:
Sim, teremos que aplicar a regra do produto. Nesse caso, temos:
Substituindo na regra do produto:
Mas como o intervalo que estamos adotando é apenas positivo, então:
Passo 3
Lembra que no passo 1 dissemos que é metade da base do retângulo? Sendo assim, a base inteira do retângulo é:
Agora que encontramos o valor de , basta substituirmos lá na função para descobrirmos quanto vale a altura do retângulo, olha só:
Sendo assim, a base do retângulo é e a altura do retângulo é .
Resposta