Um fabricante de caixas deve produzir uma caixa fechada com um volume de , onde a base é um retângulo com um comprimento três vezes maior que a largura. Ache as dimensões da caixa fabricada com o mínimo de material.
Passo 1
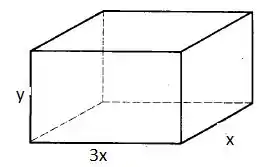
A caixa pode ser vista na ilustração abaixo. Na base temos o comprimento sendo trÊs vezes a largura. Vamos escrever o volume da caixa e da área superficial.
Passo 2
Queremos as dimensões da caixa. Para isso, vamos derivar a expressão da área dada acima em relação a x e igualar a zero.
Passo 3
Agora que encontramos o valor de vamos substituir lá naquela expressão oriunda do volume, que encontramos no passo 1.
Resposta
Portanto, as dimensões da caixa são: