Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.8 - Ex. 24
Um poster de papelão cuja figura ocupa do espaço deve ter embaixo e em cima uma margem de e uma margem de nos lados. Determine as dimensões do menor pedaço de papelão que possa ser usado para fazer o poster.
Passo 1
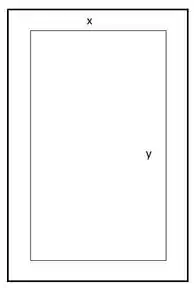
Como temos que considerar as margens da folha de papelão, as dimensões da área impressa podem ser escritas da seguinte maneira: largura sendo e comprimento . Já as dimensões da folha, contando com as margens serão: de largura e de comprimento.
Passo 2
Queremos as dimensões da menor página. Para isso, vamos derivar a expressão da área da acima em relação a x e igualar a zero.
Passo 3
Agora que encontramos o valor de vamos substituir lá naquela expressão oriunda do volume, que encontramos no passo 1.
Resposta
Portanto, as dimensões da menor página são:
Exercícios de Livros Relacionados
Uma lata fechada com um volume de 27 c m 3 deve ter a forma de um cilindro circular reto. Se a tampa e a base, ambas circulares, forem cortadas de pedaços quadrados de lata, ache o raio e a altura da
Uma fábrica sob competição perfeita (veja as intruções dos Exercícios 29 e 30 nos Exercícios 4.8) fabrica e vende rádios portáteis. A fábrica pode vender a um preço de $ 75 por rádio. Se x rádios fore
Em um armazém, mercadorias pesando 1.000 quilos são transportadas ao nível do chão, amarrando-se uma pesada corda em uma plataforma móvel, baixa, e puxando-a com um veículo motorizado. Se a corda form
Sob um monopólio (veja Exercício 31 nos Exercícios 4.8), x unidades são demandadas diariamente sendo p o preço por unidade e x 2 + p = 320 . Se o custo total da produção de x unidades for dado por C x
Se 100 x unidades de uma determinada mercadoria forem demandadas sendo p o preço por unidade, x 2 + p 2 = 36 . Ache rendimento total máximo absoluto.