Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 34
Determine o domínio e a imagem da função e desenhe um esboço de seu gráfico.
Passo 1
Observe que por se tratar de um quociente, é preciso garantir que seu denominador seja diferente de zero. Vamos determinar quando . Assim
Logo,
E também
Portanto o domínio de é
/
Passo 2
Como é uma divisão de polinômios a sua imagem será todos o números reais, ou seja, .
Passo 3
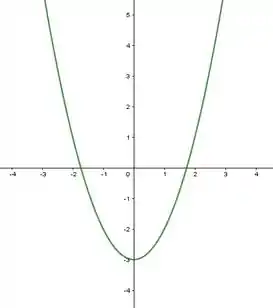
Observe que é a divisão de um polinômio do quarto grau por um do segundo grau. Assim a função é do segundo grau e seu gráfico será uma parábola. Como o coeficiente de do numerador é positivo e o coeficiente de do denominador também é positivo, temos que a parábola será côncava para cima.
Resposta
Portanto, o domínio de é /
, a imagem é e o gráfico será dado por
Exercícios de Livros Relacionados
Mostre que f x = x 3 e g x = x 3 são inversas entre si.Faça o gráfico de f e g sobre um intervalo de x grande o suficiente para mostrar que os gráficos se interceptam em ( 1,1 ) e ( - 1 , - 1 ) . Asse
Mostre que h x = x 3 / 4 e g x = 4 x 1 / 3 são inversas entre si.Faça o gráfico de f e g sobre um intervalo de x grande o suficiente para mostrar que os gráficos se interceptam em ( 2 , 2 ) e ( - 2 ,
Descubra qual gráfico corresponde a cada equação. Não utilize um dispositivo gráfico e justifique sua resposta. a )y = x 4 b )y = x 7 c )y = x 10
Uma caixa sem tampa será feita com um pedaço retangular de papelão com dimensões de 14 × 22 polegadas, cortando-se quadrados iguais de lado x em cada canto e, depois, dobrando-se as laterais para cima
Descubra qual gráfico corresponde a cada equação. Não utilize um dispositivo gráfico e justifique sua resposta. a )y = 5 x b )y = 5 x c )y = x 5