Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 84
- Mostre que e são inversas entre si.
- Faça o gráfico de e sobre um intervalo de grande o suficiente para mostrar que os gráficos se interceptam em e . Assegure-se de que a imagem mostra a simetria exigida na reta
Passo 1
Para resolvermos a letra , basta verificarmos que as duas funções são inversas. E como faremos isto??? Bem simples! Duas funções e são inversas se e somente se a seguinte relação é satisfeita:
Basta fazermos as composições das funções! Já para resolvermos a letra , precisaremos utilizar recursos tecnológicos para esboçar as nossas curvas. Esta letra é bem direta ao ponto. Basta plotarmos as duas funções e , mostrar os dois pontos de interseção entre elas e deixar claro a simetria em torno da reta . Não há muito o que ser discutido na letra .
Passo 2
Vamos começar por mostrar que as duas funções são inversas entre si. Desta forma, faremos a composição das duas funções. Temos então:
Como , as funções são inversas entre si.
Passo 3
Vamos obter os dados agora da letra . Assim temos o seguinte gráfico.
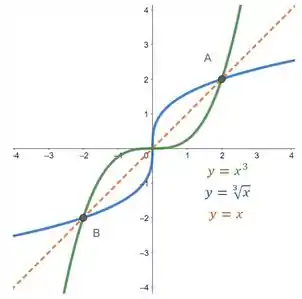
Se colocássemos um espelho em torno da reta , conseguiríamos ver claramente a simetria das duas curvas. Em destaque estão os pontos e , pontos de interseção das duas curvas.
Resposta
