Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 76
Faça o gráfico da função para e . Como o gráfico se altera à medida que é alterado.
Passo 1
Esta é uma questão que necessita de recursos tecnológicos. Portanto, esboçaremos o gráfico das nossas 5 funções (variando o valor de ) utilizando softwares. A partir das curvas obtidas, analisaremos o que acontece com elas à medida que alteramos o valor de . Isto é, verificaremos o domínio, a imagem, comportamento quando , por exemplo.
Passo 2
Vamos começar por esboçar o gráfico das nossas funções. Vejamos então abaixo:
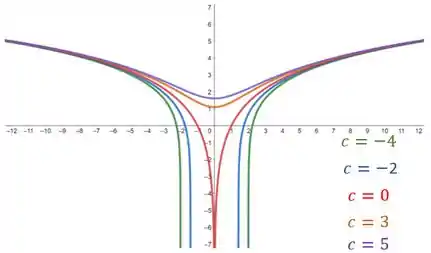
Os valores de relativo a cada curva estão relacionados com as suas cores.
Passo 3
Vamos começar a nossa análise pelo domínio da nossa função. Quando , percebemos que a nossa função se aproxima de , isto é, , mas nunca é igual a ele. Isto decorre da função , a qual possui como argumento um número maior que zero. A medida em que diminuímos o valor de , diminuímos o domínio da função. Já para , o domínio vira os reais.
Passo 4
Vejamos a agora a imagem da nossa função. Para , a imagem vai de menos infinito até mais infinito. Já à medida que adotamos um número , limitamos inferiormente o intervalo da nossa imagem. Além disto, à medida em que aumentamos o valor de , reduzimos cada vez mais o intervalo da imagem.
Passo 5
A função possui assíntotas verticais para . Já para valores maiores que zero, não há mais assíntotas verticais.
Resposta
O domínio da função diminui à medida que assumimos valores de . Já para valores maiores que zero, o domínio é constante e iguais aos reais.
Já a imagem da função, restringimos o seu intervalo quando adotamos valores de cada vez maiores e maiores que 0. Já para valores menores ou iguais a 0, a imagem é constante.
Em relação as assíntotas verticais, elas só existem para valores de .