Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.

Como temos uma raiz, a única restrição que teremos no domínio da função serão os valores onde . Desenvolvendo isso:

Tirando a raiz dos dois lados:

Ou seja:

Nosso domínio fica então

Agora vamos para a nossa imagem. Como temos uma raiz, sabemos que é pelo menos não negativa, mas temos um detalhe a mais! O está definido em um intervalo finito, ou seja, a nossa imagem também estará. Então seria errado dizer que a imagem é pois estaria faltando um limite superior nesse intervalo.

Vamos procurar o valor de que maximiza a e daí o valor da função nesse ponto será o nosso limite superior. Dá uma olhada na nossa função de novo:

Que valor de faz com que a tenha seu valor máximo? , né? Porque o termo de é . Vamos calcular para encontrar o limite superior da nossa imagem!

Agora sim temos a imagem da função:

Vamos fazer como fizemos nas últimas questões e deixar a função com uma cara mais familiar para esboçar o gráfico. Chamando de pra ficar mais fácil de entender:

Elevando os dois lados ao quadrado:

Podemos nos livrar desse módulo porque aquilo dentro da raiz já é não-negativo.

Essa equação que encontramos é uma equação especial! É a equação de uma circunferência!

Relembrando:

Onde é o raio da nossa circunferência.

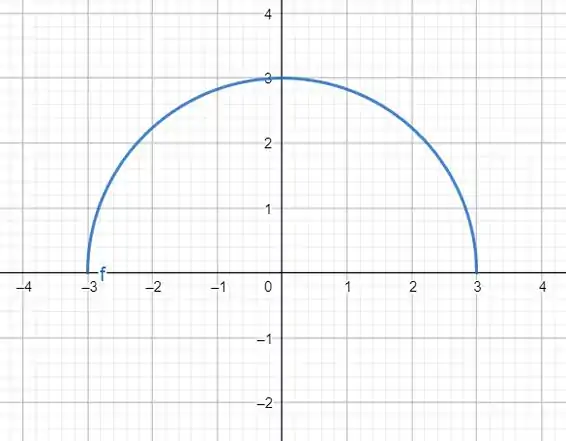
Então o nosso gráfico vai ser algo tipo uma circunferência. Não vai ser exatamente uma circunferência completa por conta da nossa imagem. Lembra que o ? Então ficaremos somente com a parte superior da circunferência. No gráfico: