Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 9g
Determine o dominio:
Passo 1
O dominio de uma função é dado pelo conjunto dos valores de onde a função está definida, ou melhor dizendo, onde não temos problemas para achar seu valor.
Como demos uma fração e NÃO EXISTE divisão por zero, então o denominador deve ser não nulo, ou seja, mas além disso, essa fração está dentro de uma raiz quadrada então devemos estudar o sinal da função.
Seja a função que corresponde á fração que está dentro da raiz, queremos apenas os valores de que são maiores ou iguais a zero.
Temos que é zero quando:
Passo 2
Assim, podemos construir uma tabela analisando o sinal de cada termo da função e a respectiva divisão dos termos que gera :
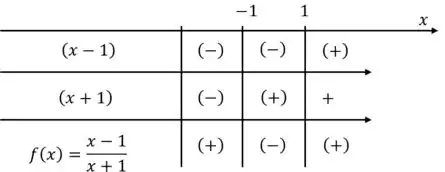
Assim, temos que:
para
Passo 3
Logo, temos que e a raiz só existe para valores e de menores que e maiores ou iguais que .
Portanto, o domínio de é: